
本书主要采用时间序列预测法计算并预测旅游市场的发展趋势。 时间序列预测法是采用预测目标的历史信息数据, 运用统计方法分析变量之间的发展变化过程的规律性,从而推测研究目标值的方法[40]。本书针对市场类型分析,采用回归分析对旅游产业的未来趋势进行市场预测, 以期获得较为精确的预测数值。
回归分析是一种数理统计方法, 它根据客观事物中诸多因素相互联系、 相互制约的特点, 通过对已掌握的大量实际数据的分析, 发现数据变化的规律性, 找出变量中的相互依存关系。 由于产业需求发展变化是由多种影响因素组成的, 而各影响因素间同时存在一定的依存关系, 因而预测产业未来需求趋势非常重要[41]。
(一) 基本原理与公式
设影响因素y的解释变量共有p个,即x1,x2,…,xp,变量之间无确定的线性关系; 设预测变量y与这些解释变量之间有线性的统计关系, 则多元线性回归模型为:
y=b0+b1x1+b2x2+…+bpxp+e,其中bi(i=0,1,…,p) 为回归系数,e为随机误差项。
若取n组数据(x1i,x2i,…,xpi;yi)(i=1,2,…,n),则这n组统计数据的机构为:
故有:y1=b0+b1x1i+b2x2i+…+bpxpi+ei(i=1,2,…,n),进行如下假设:
(1)ei~N(0,σ2),且cov(ei,ej)=0(i≠j,i=1,2,…,n);
(2) 解释变量xi(i=1,2,…,p)与随机项ej(j=1,2,…,n)不相关,也就是cov(ei,ej)=0。
当以上假定得到满足时,便可得到如下的多元线性回归模型,即,y=b0+b1x1+b2x2+…+bpxp,式中b0是常数项:bi(i=1,2,…,p)是y对xi的回归系数的估计值。
估计值b0,b1,…,bi可用最小二乘法确定,即使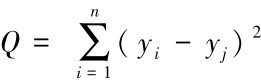
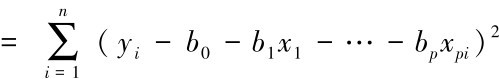 达到极小值。上式子分别对b1,b2,…,bp求导, 并分别令其为:
达到极小值。上式子分别对b1,b2,…,bp求导, 并分别令其为:
进行化简, 可得到:
由此式第一个式子可得: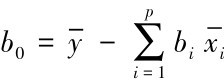
其中
将b0代入公式中的其他方程,化简后可得方程组:
其中
解出方程,可得b1,b2,…,bp,因而,多元线性回归方程为:
y=b0+b1x1+b2x2+…+bpxp
(二) 回归模型的检验
在分析多元回归时, 需检验回归模型的显著性, 包括回归方程的系数以及方程的整体相关性。从而确保预测值y与各个影响因素xi(i=1,2,…,p) 之间是否存在线性相关关系,以及每个因素xi对因变量y的实际影响。
1.可决系数R2的检验
可决系数(R2) 是衡量多元回归拟合优度的度量指标,表示因变量y中被回归模型解释的部分对y的总离差之比, 计算公式为:
其中,y为实际观测值,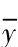 为y的平均值。可知Q残越小,R2值越接近1,则表示回归方程对数据拟合得越好, 估计方程置信度越高。
为y的平均值。可知Q残越小,R2值越接近1,则表示回归方程对数据拟合得越好, 估计方程置信度越高。
2. 回归模型的检验
在判断因变量与自变量之间的关系时, 不能确定是否线性相关, 在求回归模型时, 线性回归只是一种假设。 因此, 还需要进行F检验。
如果因变量y与所有的变量x1,x2,…,xp之间存在线性关系,一般Q残数值小,U回数值较大, 则可说明回归效果较好。 F统计量检验法通过F =
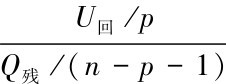 的大小衡量y与所有自变量x1,x2,…,xp之间是否存在线性相关。该比值服从自由度为(p,n-p-1) 的F分布, 其中p称为第一自由度, 代表的是回归方程中自变量的个数;(n-p-1) 称为第二自由度。
的大小衡量y与所有自变量x1,x2,…,xp之间是否存在线性相关。该比值服从自由度为(p,n-p-1) 的F分布, 其中p称为第一自由度, 代表的是回归方程中自变量的个数;(n-p-1) 称为第二自由度。
当取定显著水平为α时,查F分布表,得到Fα(n-p-1)值。若F>Fa(n-p-1),则认为y与所有变量x1,x2,…,xp之间线性关系较密切,则认为所构造的线性回归方程具有显著意义, 可预测目标值。 若某一个自变量对y的作用不显著,则在回归模型中,变量前面的系数bi就为0。可采用检验回归系数的方法来判断某个自变量xi对y是否有显著性的作用。
回归系数显著性检验 (t检验) 步骤如下:
(1)计算剩余标准差S,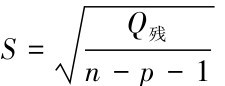 ,其中Q残为残差平方和,
,其中Q残为残差平方和,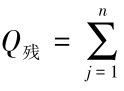
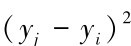 ;
;
(2)计算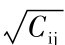 的值;
的值;
Cij是系数矩阵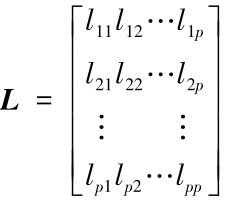 的逆矩阵L-1的i行j列元素 (i, j=1, 2, …, p);
的逆矩阵L-1的i行j列元素 (i, j=1, 2, …, p);
(3)计算统计量ti的值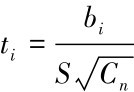 ,可证明,ti服从自由度为(n-p-1) 的t分布。
,可证明,ti服从自由度为(n-p-1) 的t分布。
(4) 给定显著水平α,查t分布表,可得t (n-p-1) 的值;
(5)判断。弱 ,则认为回归系数bi对应的xi对y有显著影响;否则,应把xi去掉,重新建立回归方程。
,则认为回归系数bi对应的xi对y有显著影响;否则,应把xi去掉,重新建立回归方程。
上一篇:典型的弹性模型和塑性模型
下一篇:指数平均数计算公式






.jpg)
