
1.3 理想气体的热力过程
在热机中,热能向机械能的转换是通过工质状态的变化即热力过程来实现的,因此对气体的热力过程进行分析是很重要的。分析气体热力过程的目的是:
(1)求出过程方程式,确定热力过程中气体状态参数的变化规律。
(2)揭示热力过程中能量变化的特性。
实际热机中的热力过程都是很复杂的,工质也是实际气体。为了便于分析,可以认为其工质都是理想气体,过程也作为可逆过程考虑,并从众多的热力过程中,抽象出几个基本热力过程(定容、定压、定温、绝热)进行分析,最后以多变过程作为普通规律进行概括。
1.3.1 定容过程
气体的比体积保持不变的热力过程称为定容过程。
1.过程方程式、参数变化关系
定容过程的过程方程式为
![]()
如图1-11a,定容过程在p-v图上是一条铅垂线。按理想气体状态方程式pv= RT,可知定容过程中状态参数的变化关系为
![]()
即定容过程中,气体的压力与温度成正比。
2.比热容、比定容热容
使单位量的物质温度升高1K需要的热量叫做比热容。
由于所取的物质单位量不相同,比热容可分为:
质量比热容,取1kg物质作为单位量。用符号M c表示,单位为kJ/(kg·K);
摩尔热容,取1kmol物质作为单位量。用符号Cm表示,单位为kJ/(kmol.K);
容积热容,取1m3(标准状况下)物质作为单位量。用c表示,单位为kJ/(m3·K)上述三种比热容的关系为:
![]()
工质的比热容随着温度的增高而稍有增大。为了简便起见,一般的热力计算中常常忽略温度对比热容的影响,而将比热容作为定值来处理,即比热容仅随工质种类而不同,称为定值比热容。
定容过程中的比热容称为比定容热容,作为定值处理时摩尔热容的数值如表1-1所示。
3.能量变化
膨胀功w
![]()
吸热量q
在定容过程中,根据比热容的定义,有
![]()
比热容取定值时
![]()
热力学能变化量Δu
根据热力学第一定律
![]()
即定容过程中工质吸收的热量全部用来增加其热力学能。
对于理想气体,由于分子间没有作用力,故分子之间没有位能,理想气体的热力学能就仅与分子平均动能有关,即其热力学能仅与温度有关,而与比体积无关,即
![]()
由于理想气体的热力学能仅是温度的单值函数,它只与初始状态的温度有关而与过程无关,所以当cv取定值时,对任何过程都有
Δu= cvΔT或du= cv dT
4.熵的变化量Δs
根据熵的定义式,并取cv为定值,有
![]()
即定容过程中,随温度的变化,工质的比熵按对数函数变化,在T-s图中,过程为一指数曲线。如图1-11b所示。
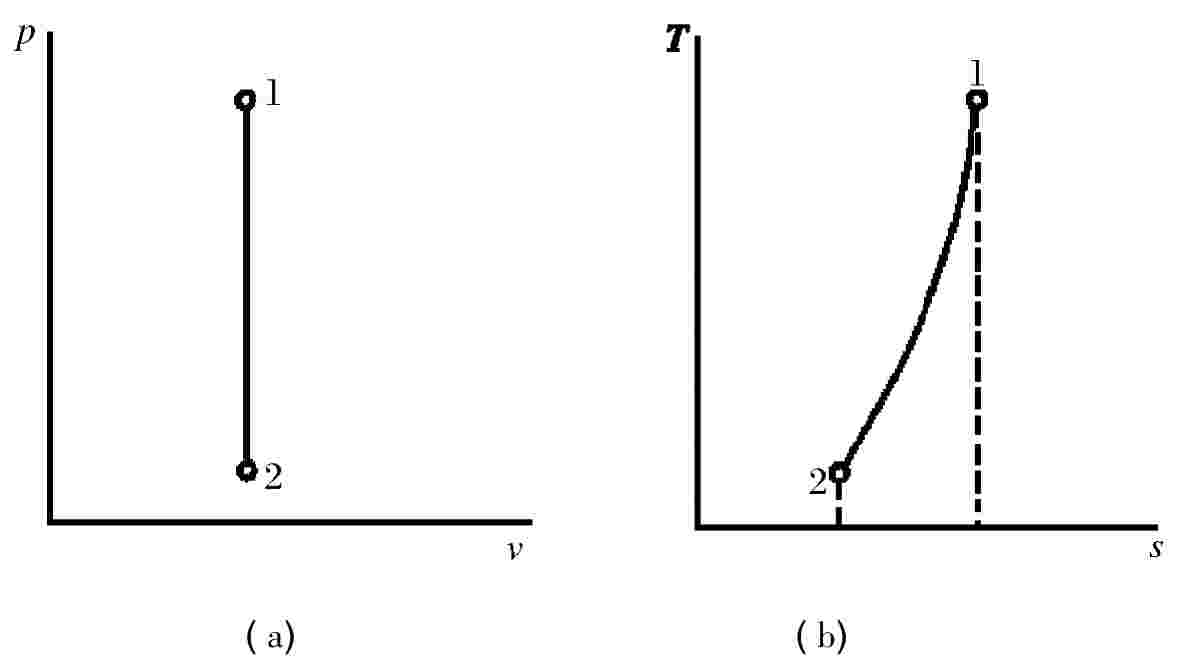
图1-11 定容过程
1.3.2 定压过程
气体的压力保持不变的热力过程称为定压过程。
1.过程方程式、参数变化关系
定压过程的过程方程式为
![]()
如图1-12a,定压过程在图上是一条水平线。按理想气体状态方程式,可知定压过程中状态参数的变化关系为
![]()
即定压过程中,比体积与温度成正比。
2.比定压热容
定压过程中的比热容称为比定压热容,用cp表示。作定值考虑时,其摩尔热容的数值如表1-1所示。
表1-1 理性气体的定值摩尔热容和比热比
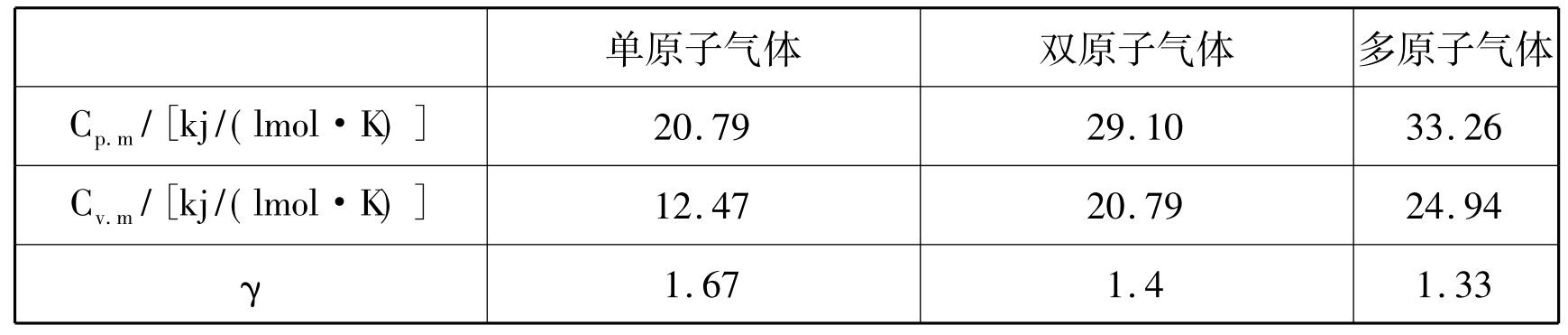
根据表中数据,结合气体的千摩尔质量即可得到cp与cv。
由于h= u+ pv= u+Rg T
对T求导
![]()
![]()
![]()
式(1-27)和式(1-28)叫做迈耶公式,它给出了理想气体cp与cv及Cp.m与Cv.m的关系。
cp与cv之比叫做比热比或绝热指数,用符号γ表示。
![]()
![]()
![]()
3.能量变化
膨胀功w
![]()
吸热量q
在定压过程中,有cp= dq/dT,比热容取定值时
![]()
焓的变化量Δh
根据热力学第一定律,过程可逆时有
![]()
![]()
即等压过程中工质吸收的热量全部用来增加工质的焓。
对于理想气体h= u+ pv= u+Rg T
所以焓也仅仅是温度的单值函数。当cp取定值时,对任何过程都有
Δh= cpΔT或dh= cp dT
4.熵的变化量Δs
cp取定值,有
![]()
定压过程中,随温度的变化,工质熵的变化与定容过程很类似。在T-s图中,过程也为一指数曲线,如图1-12(b)。由于cp>cv,所以定压线比定容线平缓。
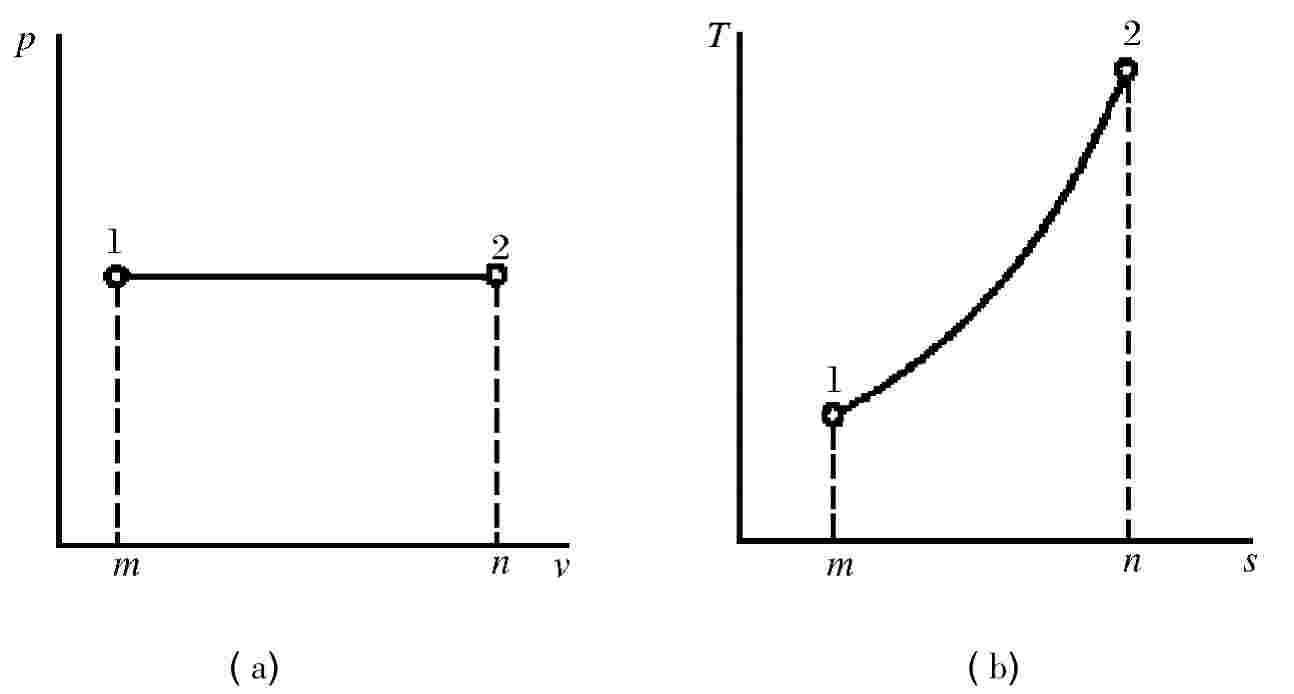
图1-12 定压过程
1.3.3 定温过程
气体的温度保持不变的热力过程成为定温过程。
1.过程方程式、参数变化关系
定温过程的过程方程式为
![]()
如图1-13,定温过程在p-v图上是一条双曲线。在T-s图上是一条水平线。根据理想状态方程式,由pv= const,得
![]()
即定温过程中,压力与比体积成反比。
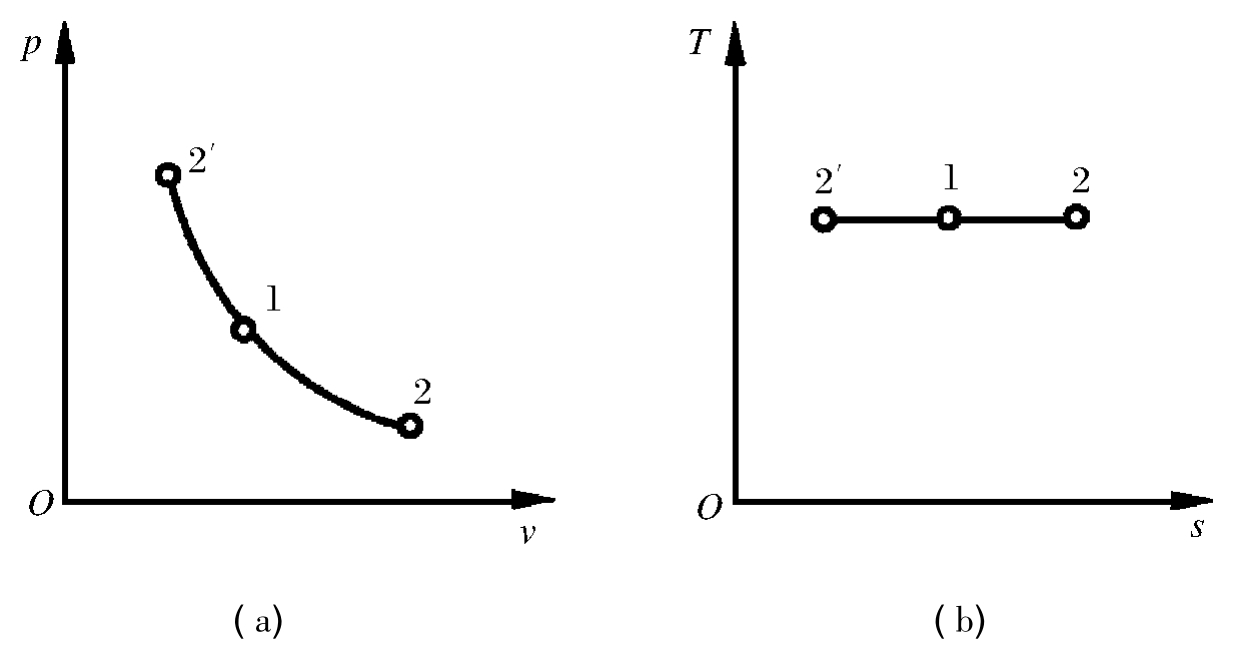
图1-13 定温过程
2.能量变化
膨胀功w
![]()
热力学能,焓的变化量Δu,Δh
因为dT= 0
所以du= cv dT= 0
dh= cp dT= 0
吸热量q
因为Δu= 0,根据热力学第一定律,有
![]()
因为Δh= 0,根据热力学第一定律,ws= q=w,即定温过程轴功等于膨胀功。
3.熵的变化量Δs
![]()
1.3.4 定熵过程
气体与外界没有热量交换的热力过程称为绝热过程。
1.过程方程式、参数变化关系
由定义知,绝热过程中dq= 0
过程可逆时 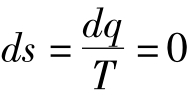
可逆的绝热过程也叫做定熵过程。
所以热力学第一定律可写为
dq= du+ dw= cv dT+ pdv=0
而 pv=Rg T
求微分得 pdv+ vdp=Rd T
代入上式,整理得
(cv+Rg)pdv+ cv vdp= 0
因为 cp= cv+Rg γ= cp/cv
所以有 γpdv+ vdp= 0
即 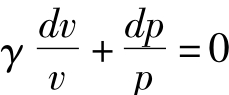
当cp、cv为定值时,γ也为定值。对上式积分,得
![]()
式(1-41)就是定熵过程的过程方程式。在p-v图上,定熵过程是一条高次双曲线,与定温过程方程式相比较,可知定熵过程的曲线更陡些。在T-s图上,它是一条铅垂线,如图1-14所示。
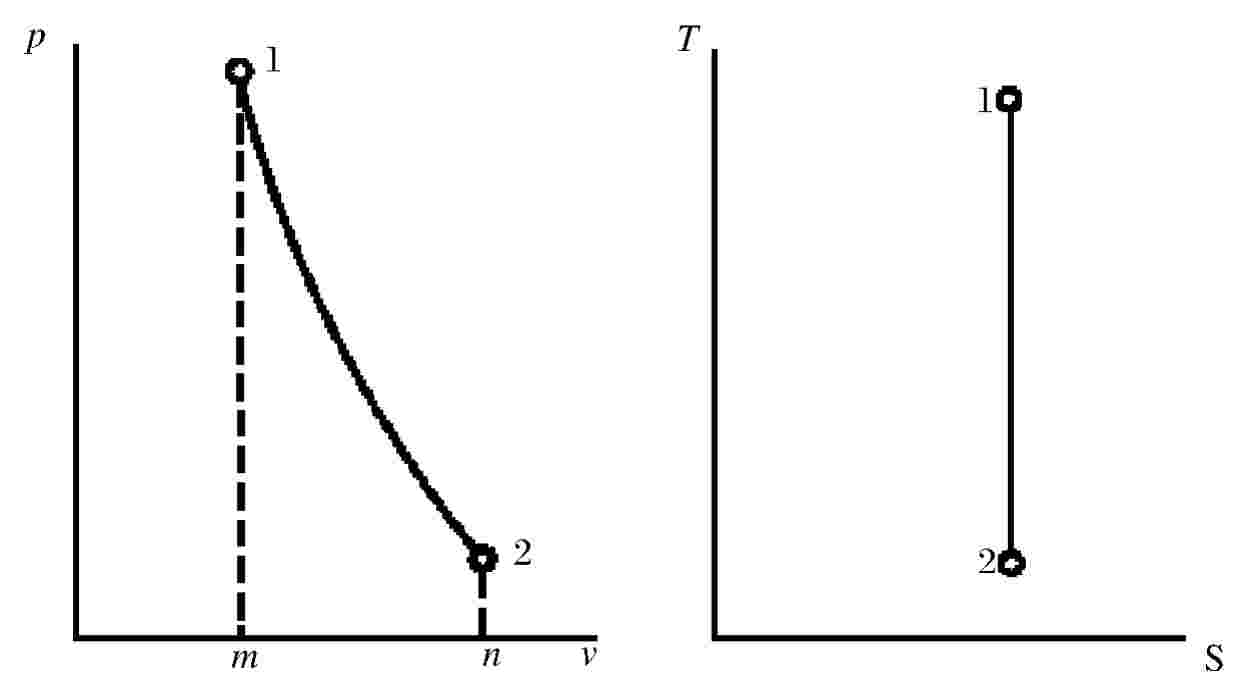
图1-14 定熵过程
气体在定熵过程中初态和终态间状态参数之间的关系可从过程方程式和状态方程式导出。

可见,当气体作定熵膨胀,其温度和压力都是下降的。
2.能量变化
吸热量q= 0
膨胀功w、热力学能变化量Δu
![]()
或写成
![]()
轴功ws,焓的变化量Δh
![]()
或写成
![]()
1.3.5 多变过程
上述四种典型热力过程的特征是,某一个状态参数保持不变,而实际的过程往往是所有的参数都在变化,但这些状态变化一般遵循一定的规律。此时,过程方程式可通过实验,测定过程中一些状态点的p、v值而近似地整理成pvn=定值的形式。这样的过程叫多变过程,式中指数n叫做多变指数。在某一多变过程中,n为一定值,但不同多变过程的n值各不相同。对复杂的实际过程,可将其分为几段不同多变指数的多变过程来描述,每一段中的n值不变。由此可见,多变过程是一些有规律的过程的总称。这些过程的特征是:在整个过程中:
![]()
其中n为常数。
前面所述的四种典型热力过程可视为多变过程的特例之一,即:
当n= 0时,pv0= p= const,即定压过程;
当n= 1时,pv1= pv= const,即定温过程;
当n=γ时,pvγ= const,即定熵过程;
当n=±∞时,pv1= const,可写为pv1/n= const,则n=±∞时,v= const,即定容过程。
多变过程的多变指数可在0~±∞间变化,当多变指数为某一确定的值时,过程的特性也就确定了。在热力设备通常进行的热力过程中,n值不会为负值。
1.过程方程式、参数变化关系
式(1-49)即为多变过程的方程式。
根据pvn= const和pv=Rg T,得其参数变化关系为

2.能量变化
膨胀功w
多变过程中气体所做的膨胀功
![]()
或
![]()
轴功ws
由于pvn= const,微分后可得npdv=-vdp,轴功
![]()
对比式(1-55)和式(1-53)可见,在多变过程中,轴功ws为膨胀功w的n倍。
多变过程的吸热量

根据比热容的定义,多变过程的比热容(多变比热容)c为
![]()
当n= 0时,c=γcv= cp,即定压过程比热容;
当n= 1时,c=±∞,即定温过程比热容;
当n=γ时,c= 0,即定熵过程比热容;
当n=±∞时,c= cv,即定容过程比热容。
3.熵的变化量Δs的计算
先看任意过程时的
在可逆过程中,有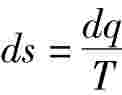
且有 dq= du+ dw= cv dT+ pdv
dq= du-dws= cp dT+ vdp
代入上式得
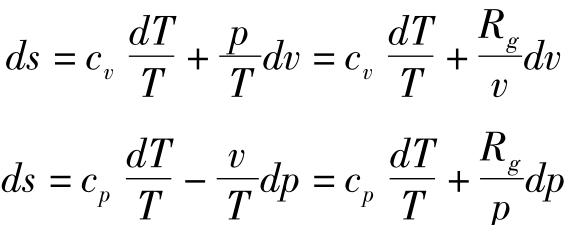
积分,得

比热容为定值时,则可写为

又因 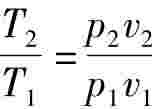
取对数 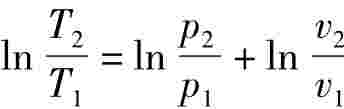
代入式(1-60),则有
![]()
公式(1-60)、(1-61)、(1-62)是在过程可逆、定值比热容的条件下推导出来的,但由于熵是状态参数,故无论过程可逆与否,上述三式都适用。
取定值比热容,则多变过程中Δs为
![]()
将多变过程方程式代入式(1-62)也可得到这个结果。
4.多变过程在p-v、T-s图上的表示
四种典型过程在p-v、T-s图上的曲线形状前已述及,如图1-15所示。为了便于分析多变过程中的能量分配关系,以上述四个典型过程曲线为界,在图1-15上划分出了功、热量和热力学能变化的正、负区域。
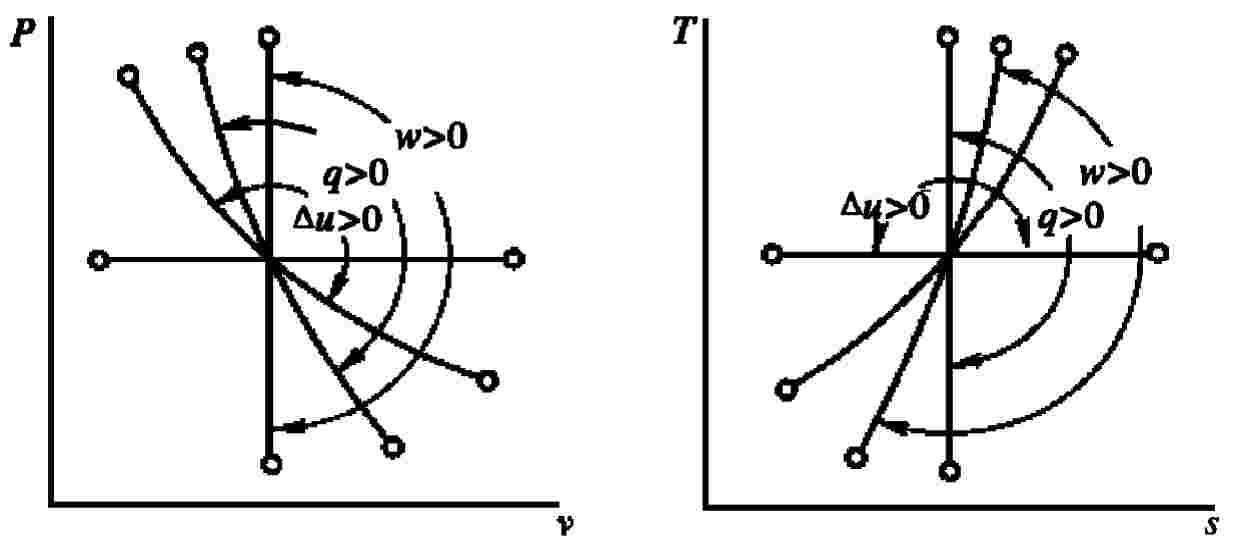
图1-15 多变过程示意图
在任一多变过程中,n为一确定值,它在p-v图、T-s图上就有一确定的位置,它的能量分配关系也就确定了。
上一篇:工作经验总结精彩标题大汇总
下一篇:详图索引符号和详图符号怎么绘制





.jpg)
.jpg)
