单缝夫琅禾费衍射

    1821年，夫琅禾费（J．von Fraunhofer）研究了一种单缝衍射，如图8.19（a）所示，单色平行光垂直照射于宽度为a的狭缝AB上，根据惠更斯-菲涅耳原理，单缝所在处的波面上各点都是相干的子波源，它们向各个方向发射的光为衍射光，沿某一方向传播的衍射光与衍射屏法线之间的夹角θ称为衍射角．具有相同衍射角的光线经过透镜L聚焦于屏幕上同一点，不同衍射角的光线会聚在屏上不同点，形成一组平行于狭缝的明暗相间的直条纹，如图8.19（c）所示．

    图8.19　单缝夫琅禾费衍射

    下面用菲涅耳半波带法研究屏幕上的衍射图样．

    设入射光波长为λ，先来考虑沿入射方向传播、对应衍射角θ=0的衍射光，经透镜L后这束光会聚于O点，见图8.19（a）光束①．由于AB是同相面，透镜又不会引起附加的光程差，它们到达O点时仍保持相同的相位，从而相互加强，该位置对应中央明纹的中心．

    下面讨论衍射角为θ的任一衍射平行光束，如图8.19（a）光束②，该光束各条光线到达Q点的光程并不相等，但垂直于各光线的BC面上各点到达Q点的光程相等，故这束光中单缝边缘A、B两点发出的光线光程差最大，为

    

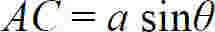
    图8.20　菲涅耳半波带法

    上述分析可用数学方式表述如下，当衍射角θ满足

    时，对应点处为暗纹中心，对应于k=1，2，…，分别为第一级暗纹，第二级暗纹，…，式中正、负号表示条纹对称分布于中央明纹两侧．而当衍射角θ满足

    时，对应点处为明纹中心，对应于k=1，2，…，分别为第一级明纹，第二级明纹，…，应指出上式不包括k=0的情形，对式（8.21b）来说，k=0虽对应于一个半波带形成的亮纹，但仍处在中央明纹范围内，是中央明纹的一个组成部分．值得注意的是，上述两式与杨氏双缝干涉条纹的条件，在形式上正好相反，不要混淆．

    由干涉图样可以看到各级明纹有一定宽度，常将两暗纹之间的距离视为明纹的宽度，相邻暗纹对透镜中心所张的角为明纹的角宽度．由式（8.21）可求出明纹的宽度，中央明纹宽度为两侧的第一级暗纹间距，如果衍射角很小，由式（8.21a），第一级暗纹距中心O的距离为

    

    

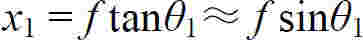
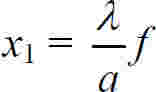
    中央明纹宽度为

    

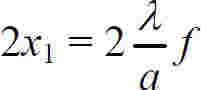
    其他相邻明纹的宽度为

    图8.21　单缝衍射图样相对光强分布

    由式（8.21）可知，对于一定波长的入射光，缝宽a越小，各级条纹的衍射角θ越大，屏上条纹的间距也越大，即衍射效果越明显．反之缝宽a增大，各级条纹的衍射角θ变小，各级条纹向中央明纹靠拢，当a增大到一定程度至条纹密不可辨时，衍射现象消失，此时光可看作是直线传播的．可见光的直线传播是障碍物线度远大于光波长时衍射效果不显著的情况．

    例8.7　在单缝夫琅禾费衍射实验中，缝宽a=5λ，缝后透镜焦距f=40cm，试求中央明纹和第一级明纹的宽度．

    解　设第一级、第二级暗纹对应的衍射角分别为θ1和θ2，由单缝衍射的暗纹条件可知

    第一级暗纹距中心O的距离为

    第二级暗纹距中心O的距离为

    由此可得中央明纹的宽度为

    

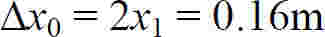
    第一级明纹的宽度为

    例8.8　在单缝衍射实验中，若光源发出的光含有两种波长λ1和λ2，且已知λ1的第一级暗纹与λ2的第二级暗纹相重合．试求：（1）λ1和λ2之间的关系；（2）这两种光形成的衍射条纹中，是否还有其他暗条纹相重合？

    解　（1）由单缝衍射的暗纹条件可知

    由题意知，θ1=θ2，所以有λ1=2λ2．

    （2）对波长为λ1的单色光，单缝衍射的暗纹条件为

    将λ1＝2λ2代入

    asinθ1＝k1λ1＝2k1λ2，　　　　k1＝1，2，3…

    波长为λ2的入射光的单缝衍射暗纹条件为

    asinθ2＝k2λ2，　　　　k2＝1，2，3…

    显然，对于k2＝2k1的各级暗纹来说，θ1＝θ2，即相应暗纹重合．