自适应卡尔曼滤波

    8.1.2　自适应卡尔曼滤波

    随着观测数据的增加，状态估计应越来越精确，但实际应用中，滤波所得状态估计值和实际状态之间的误差，远远超过了理论估计值，这种现象称为滤波的发散，从而也使滤波失去了最佳作用，因此必须予以克服。

    自适应滤波通过不断利用新信息，修正滤波的原有设计，降低滤波误差，从而达到抑制发散的目的。假设存在一个偏差b，则滤波模型式(8-1)变为:

    

    式中，B_k、C_k为b对动态模型和观测模型的影响矩阵，噪声的统计特性不变。

    上述模型的处理方法有两种:一种是在原模型的状态空间中增加一些表示偏差项的元素，利用滤波公式一并对偏差和状态向量做估计，即一步卡尔曼滤波;另一种是直接利用不含偏差项的滤波结果，对每个可能的偏差项作出估计，即两步卡尔曼滤波。

    1.一步滤波法

    一步滤波法将偏差b看作状态向量的一部分附加到原有的状态向量X中，一起参与平差计算，合并后的状态向量Y=(X，b)^T，则式(8-1)变形为:

    

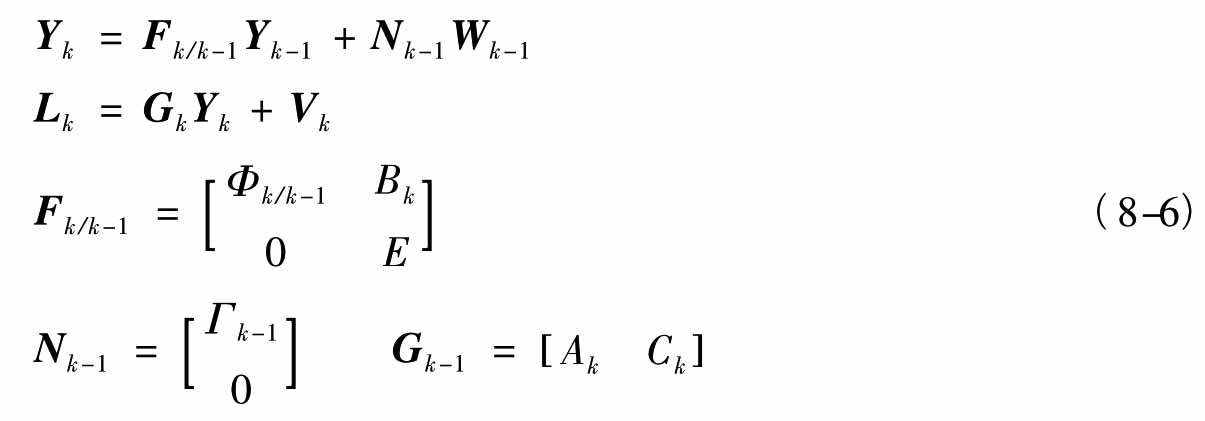
    利用式(8-2)～式(8-4)，解算Y，便得到了b。

    一步卡尔曼滤波模型简单，但对先验统计特征要求严格，并非真正意义上的自适应滤波。

    2.两步自适应滤波

    两步卡尔曼滤波克服了一步滤波的缺陷，适合后续的质量控制和滤波递推。首先通过一般的卡尔曼滤波，对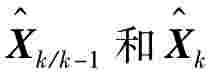进行估计，并检验是否存在偏差b，若存在，进行第二步滤波。根据Frieland1969年和Lgnagni1981年的观点，b对估值的影响是线性的，故有:

    

    式中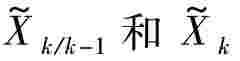，代表带有偏差的状态预测值和滤波值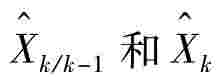，代表无偏差的状态预测值和滤波值。

    根据式(8-7)，无偏差模型和有偏差模型所得残差预报之间关系为:

    

    式中，r(k)和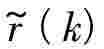分别代表无偏差模型和有偏差模型的预报残差。U_k、V_k、S_k代表敏感矩阵，可由下列递推公式确定:

    

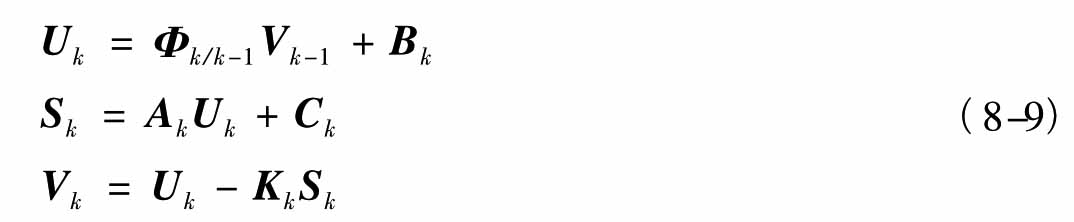
    敏感矩阵确定下来之后，便可进行第二步卡尔曼滤波，其递推过程如下:

    

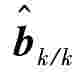    确定后，对进行修正，则顾及偏差影响的状态最优预测和滤波估值为:

    

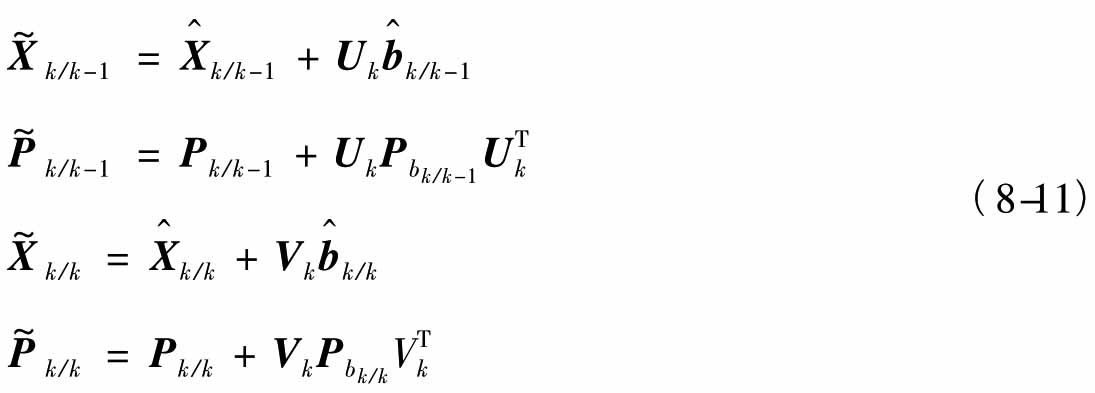
    第k个历元的两步滤波完成后，便可进行下一个历元的滤波。

    由于测量中不可能每个历元都存在偏差。为了提高滤波效率，需先定位偏差，再做自适应滤波。

    3.预测残差χ²检验偏差

    该法是根据检验统计量T_G确定接受或拒绝法则，设d为χ²分布的自由度，则:

    

    设r为预报残差，从l历元开始，由后续n个历元得到残差序列为r=(r_l，r_{l+ 1}，…，r_{l+ n})，r～N(0，Q_r)。若r无偏，则服从正态分布，为零均值，否则，不为零均值，且偏离量为S_r b，即r～N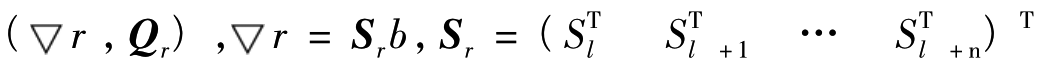。则T_G为(李德仁，1988):

    

    若n= 0，则有:

    

    式(8-14)表明，仅利用当前的观测信息即可进行偏差检验，即局部预警检验。

    4.偏差定位和自适应消除

    数据探测是对每个假设检验的偏差源分别进行定位检验，直到检验到全部可能的偏差。

    根据式(8-13)，仅利用当前信息进行局部检验，在H₀下有:

    

    综上所述，自适应卡尔曼滤波的计算流程可分为四个阶段。

    (1)第一步滤波。利用式(8-2)～式(8-4)，进行一般卡尔曼滤波。

    (2)偏差检验。根据外部测量信息和系统输出信息构筑残差序列，并根据该序列构建统计量，在χ²分布下执行假设检验，判断是否存在偏差。

    (3)偏差定位。若探测到偏差，启动备选假设，利用式(8-6)，逐一进行诊断定位，将最有可能的偏差识别出来。

    (4)第二步滤波。若定位了偏差，则根据式(8-9)、式(8-10)确定偏差量，根据式(8-11)进行第二步滤波，在第一步滤波的结果中消除偏差对X_k及P_k的影响，实现对偏差的修正。

    上面介绍了卡尔曼滤波基本原理。卡尔曼滤波为组合导航系统信息融合提供了理论支持，在此基础上，下面介绍不同的水下组合导航系统。