
4.3 局部搜索算法和最优化问题
我们已经讲过的搜索算法都是设计用来系统化地探索搜索空间的。它们在内存中保留一条或多条路径并且记录哪些是已经探索过的,哪些是还没有探索过的。当找到目标时,到达目标的路径同时也构成了这个问题的一个解。
然而在许多问题中,到达目标的路径是无关的。例如,在八皇后问题中(参见第3.2.1节),重要的是最终皇后的布局,而不是加入皇后的次序。这一类问题包括了许多重要的应用,例如集成电路设计,工厂场地布局,作业车间调度,自动程序设计,电信网络优化,车辆寻径,文件夹管理。
如果到目标的路径是无关的,我们将考虑不同种类的算法,这类算法根本不关心路径。局部搜索算法从单独的一个当前状态(而不是多条路径)出发,通常只移动到与之相邻的状态。典型情况下,搜索的路径是不保留的。虽然局部搜索算法不是系统化的,但是它们有两个关键的优点:(1)它们只用很少的内存——通常容量是一个常数;(2)它们经常能在不适合系统化算法的很大或无限的(连续的)状态空间中找到合理的解。
除了找到目标,局部搜索算法对于解决纯粹的最优化问题是很有用的,其目标是根据一个目标函数找到最佳状态。许多最优化问题不适合第三章中介绍的“标准的”搜索模型。例如,自然界提供了一个目标函数——繁殖适应性——达尔文的进化论可以被视为优化的尝试,但是这个问题没有“目标测试”和“路径耗散”。
为了更好地理解局部搜索,我们会发现考虑状态空间地形图(如图4.10所示)是很有用的。地形图既有“位置”(用状态定义)又有“高度”(由启发式耗散函数或目标函数的值定义)。如果高度对应于耗散,那么目标是找到最低谷——即一个全局最小值;如果高度对应于目标函数,那么目标是找到最高峰——即一个全局最大值。(我们可以通过插入一个负号使两者相互转换。)局部搜索算法探索这个地形图。如果存在解,那么完备的局部搜索算法总能找到解;最优的局部搜索算法总能找到全局最小值/最大值。
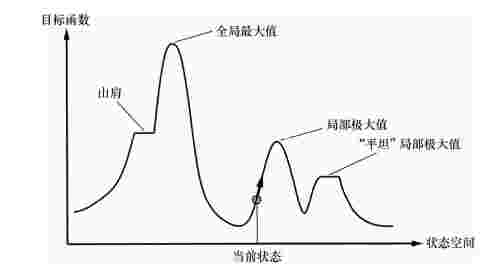
图4.10 一维空间的状态空间地形图,高度对应于目标函数。目标是找到全局最大值。如箭头所示,爬山法搜索修正当前状态并试图改进它。各种地形特征在教材中有定义
下一篇:家庭体育在全民健身中的重要作用





.jpg)
.jpg)
