置信区间和预测区间怎么求

    1.7.7　参数估计——区间估计

    对于未知参数，用某个区间来估计，这称为区间估计.未知参数θ的区间估计记作在随机抽样前，求区间估计即是构造区间的两个端点θ=f₁(X₁，…，X_n)=f₂(X₁，…，X_n);在随机抽样后，把样本值(即数据)代入端点公式便得θ的估计区间.

    1.置信区间

    置信区间是区间估计中最常用的形式.

    设样本X₁，…，X_n取自总体X，θ是未知参数.如果都是样本X₁，…，X_n的函数，且对于给定的1－α(0＜α＜1)满足

    

    那么称随机区间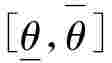是置信度(或置信水平)为1－α的置信区间.通常取1－α为90%、95%、99%(即相应的α=10%、5%、1%)等.

    置信区间中的概率P(的可信程度，概率越大，可信程度越高，区间估计越佳.另一方面，置信区间的长度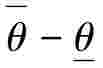反映区间估计的精度，长度越短，精度越高，区间估计越佳.

    2.单个正态总体中未知参数的置信区间

    设总体X服从N(μ，σ²).X₁，…，X_n是取自正态总体X的样本.给定置信度1－α.

    (1)数学期望的置信区间

    ①当方差σ²=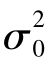已知时，数学期望μ的置信度为1－α的置信区间是

    

    其中λ满足P(|U|≤λ)=1－α，U服从N(0，1).

    ②当方差σ²未知时，数学期望μ的置信度为1－α的置信区间是

    

    其中λ满足P(|T|≤λ)=1－α，T服从t(n－1).

    (2)方差与标准差的置信区间

    设数学期望μ未知.方差σ²的置信度为1－α的置信区间是

    

    标准差σ的置信度为1－α的置信区间是

    

    其中λ₁，λ₂满足P(χ²＜λ₁)=P(χ²＞λ₂)=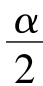，χ²服从χ²(n－1).

    3.两个正态总体中均值差与方差比的置信区间

    设总体X～N(μ₁，.X₁，…，X_n1是取自正态总体X的样本，Y₁，…，Y_n2是取自正态总体Y的样本.给定置信度1－α.

    (1)均值差μ₁—μ₂的置信区间

    设，但未知.μ₁—μ₂的置信区间的两个端点是

    

    其中λ满足P(|T|≤λ)=1－α，T服从t(n₁+n₂－2).

    (2)方差比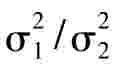的置信区间

    设μ₁、μ₂均未知.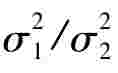的置信区间是

    

    其中λ₁、λ₂满足P(F＜λ₁)=P(F＞λ₂)=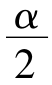，F服从F(n₁－1，n₂－1).

    【例1.7-38】对某一距离进行5次独立测量，得数据(单位:m)如下:

    1250，1265，1245，1275，1260.

    已知测量值无系统误差，即可以认为测量值服从正态分布N(μ，σ²)，其中μ，σ²均未知.在置信度0.95下求μ与σ的置信区间.

    解:由所给数据算得=1259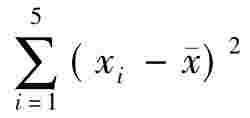，=570，s=11.94.

    对于数学期望μ的置信区间，由n－1=4，α=0.05查t分布(自由度为4)临界值表，得到λ= 2.78.于是，由

    

    得到μ的置信区间为［1244.2，1273.8］.

    对于标准差σ的置信区间，由n－1=4，α=0.05查χ²分布(自由度为4)临界值表，得到λ₁=0.484，λ₂=11.1.于是，由

    

    得到σ的置信区间为［7.2，34.3］.