
如何证明三点共线
黄金殿
在初中几何教学中,遇到证明三点共线的习题较多。概括起来有两类:一类是直接证明三点共线的习题,另一类是证明某个结论需要证明三点共线的习题。这两类习题在教材中出现不多,但证法不易掌握,很多学生无处下手。现总结证明方法如下。
一、应用平行公理证明
(平行公理:经过直线外一点,有且只有一条直线与这条直线平行)
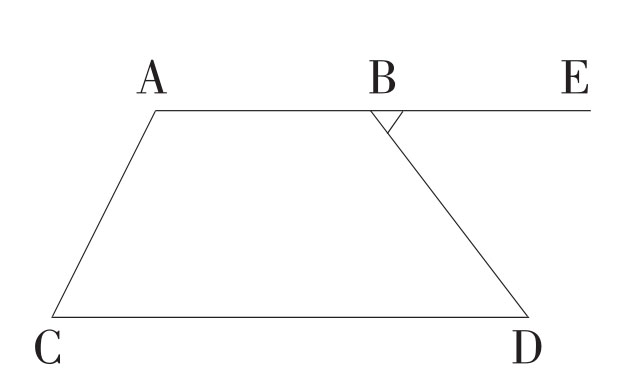
例1 已知如图,∠A+∠C=180°,∠1=∠2。
求证:A、B、E三点共线。
证明:∵∠A+∠C=180°(已知)A B
∴AB//CD(同旁内角互补,两直线平行)。
∵∠1=∠2(已知)
∴BE//CD(内错角相等,两直线平行)CD
∴A、B、E三点在一条直线上。
二、应用平角定义
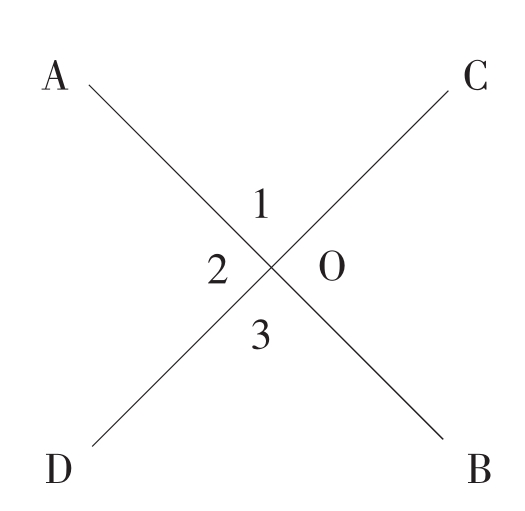
例2 已知如图,COD是直线,∠1=∠3。
求证:A、O、B三点在一条直线上。
证明:∵COD是一条直线。
∴∠1+∠2=180°(平面定义)。
∵∠1=∠3,∴∠2+∠3=180°。
∴A、O、B三点在一条直线上(平角定义)。
三、应用垂线的性质D
(垂线性质:过一点有且只有一条直线与已知直线垂直)
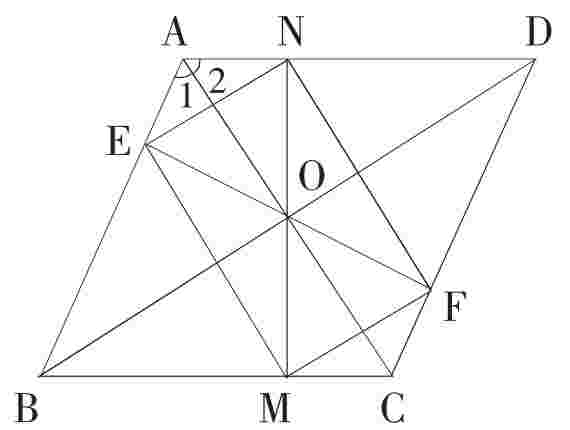
例3 已知,菱形ABCD,对角线AC、BD相交于点O,ON⊥AD,OM⊥BC,OE⊥AB,OF⊥CD,点N、M、E、F分别为垂足。
求证:四边形EMFN是矩形。
证明:∵四边形ABCD是菱形。
∴AD//BC.
∵OM⊥BC,∴OM⊥AD。
又∵ON⊥AD,过O只能作一条直线垂直于AD。
∴M、N、O在一条直线上。
同理E、F、O也在同一条直线上。
∵在菱形ABCD中,∠1=∠2(菱形性质定理2)。
又∵OE⊥AB,ON⊥AD,∴OE=ON。
同理OE=OM.OM=OF,∴OE=OF,OM=ON。
∴四边形EMFN是平行四边形(平行四边形判定定理3)。
∴OE+OF=OM+ON,即EF=MN。
∴EMFN是矩形(对角线相等的平行四边形是矩形)。
(载《现代中学生》2007年第10期)





.jpg)
.jpg)
