定的雪橇合力的大小或方向也要同时发生突变

    6　狗拉雪橇——合力原理

    知识导航

    在国外的雪场上，狗拉雪橇属于一种贵族娱乐。通常，拉雪橇的狗都是纯种西伯利亚哈士奇、阿拉斯加雪橇犬或者萨摩耶。即使雪橇上站着一个胖子，雪橇也会在一群拉雪橇的狗的合力作用下，在雪地里向前急驰而去。合力作用在物理学中，被系统地发展为合力原理进行学习和研究。狗拉雪橇的合力向着前进的方向，地面的摩擦力方向与之相反，只有狗拉雪橇的力大于地面摩擦力才能够拉动雪橇。如果狗拉雪橇的合力与前进方向不太一致，出现一定的角度，我们该怎样计算这个合力呢？物理学中就有很好的解答。

    无论雪橇狗的体态是胖是瘦，体型是大是小，只要和其他的狗在一起拉一个雪橇，那么，这个狗出的力就属于合力的一部分，即使它使出的力与合力的方向是相反的。如果要用一句话来概括狗拉雪橇的真谛，那就是“团结就是力量”。

    

    团结就是力量——狗拉雪橇

    在物理学中，合力原理指的就是著名的牛顿第二定律：物体的加速度与其所受的外力成正比，与物体的质量成反比，加速度的方向和合外力的方向相同。我们可以用数学表达式将合力写成F_合=kma。其中，k是一个常数，但由于当时没有规定1个单位的力的大小，于是取k=1，就有了F=ma这个公式，这也就是我们今天比较熟悉的牛顿第二定律的表达式。

    知识放大镜

    合力为零与没有合力有区别吗？

    我们在物体的受力分析中，经常会听到这样的力学术语，比如，“合力为零”和“没有合力”。那么，“合力为零”与“没有合力”是一种情况吗？我们知道单个力作用在物体上，它会产生运动。我们从合力的概念中知道，合力实质上是一个单力，它具有力的三要素，即大小、方向和作用点。“合力为零”实质上是一种“等效单力”，大小是零，方向和作用点都存在。如果它虽然大小和方向确定，没有作用点，那么我们就认为它不存在合力。“合力为零”与“没有合力”是两个不同的力学概念，没有合力并不是合力为零。

    下面，我们将分别从牛顿第二定律的含义和性质出发，予以系统地介绍：

    牛顿第二定律的含义可以大致概括为三个方面。第一，牛顿第二定律是力的瞬时作用规律，力和加速度同时产生，同时变化，同时消失；第二，F=ma是一个矢量方程，应用时应规定正方向，凡与正方向相同的力或加速度均取正值，反之取负值，一般常取加速度的方向为正方向；第三，根据力的独立作用原理，用牛顿第二定律处理物体在一个平面内运动的问题时，可将物体所受各力正交分解，在两个互相垂直的方向上分别应用牛顿第二定律的分量形式：Fx=max，Fy=may列方程。通个这个公式的介绍，就可以很好地解决力量不在一条直线上的问题。

    牛顿第二定律大概有六个主要性质。第一，因果性：力是产生加速度的原因。若不存在力，则没有加速度。第二，矢量性：力和加速度都是矢量，物体加速度方向由物体所受合外力的方向决定。第三，瞬时性：当质量一定的物体所受外力发生突然变化时，作为由力决定的加速度的大小或方向也要同时发生突变；当合外力为零时，加速度同时为零，加速度与合外力保持一一对应关系。牛顿第二定律是一个瞬时对应的规律，表明了力的瞬间效应。第四，相对性：自然界中存在着一种坐标系，在这种坐标系中，当物体不受力时将保持匀速直线运动或静止状态，这样的坐标系叫惯性参照系。地面和相对于地面静止或作匀速直线运动的物体可以看作是惯性参照系，牛顿定律只在惯性参照系中才成立。第五，独立性：物体所受各力产生的加速度，互不干扰，而物体的实际加速度则是每一个力产生加速度的矢量和，分力和分加速度在各个方向上的分量关系，也遵循牛顿第二定律。第六，同一性：a与F与同一物体某一状态相对应。当物体的质量m一定时，物体所受合外力F与物体的加速度a成正比是错误的，因为是合力决定加速度。但当说是物体的质量m一定时，物体的加速度a与物体所受合外力F成正比是正确的。

    

    

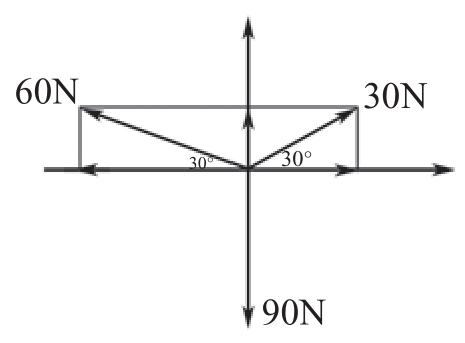
    力的正交分解

    简单来说，合力就是作用在物体上所有的力产生的总效果，这些力包括了物体系统内部的相互内力和受到的外部外力，我们将这些力产生的总效果表现出来，就是物体所受到的合力。一般我们将合力划分到某个方向，便于研究问题，但实际上它是不存在的力。因为根据力的定义可得，力是物体之间的相互作用。几个力的合力是找不到真正的施力物体的，所以它不是实际存在的，而是人为定义出来的。

    知识扩展

    了解力的正交分解

    我们通常将一个力分解为两个相互垂直的分力的方法，叫作“力的正交分解”。

    物理学上，利用力的正交分解法求合力的步骤：

    第一步是选定研究对象，并且以质点的形式对其进行表示；第二步是对选定的研究对象进行受力分析；第三步是建立直角坐标系。一般来讲，在水平面内，我们可以任意建立坐标系，但如果在斜面上最好沿着物体运动的方向建立X轴和Y轴；第四步是分析物体加速度的方向（必要时也可将加速度进行正交分解，以便做题）；第五步是表达合外力；第六步是列出X轴的方向、Y轴方向以及牛顿第二定律方程；第七步，如果需要其他方程，也应该列出需要的方程，然后进行求解；最后一步是检验求解过程和结果是否符合实际情况。

    实际生活或工作中，我们在处理力的合成和分解问题时，常运用力的正交分解法。这是一种很常用的方法，但是在运用时需要注意以下几点：

    第一点，合力是矢量F，其在X轴和Y轴上的分力也是矢量，称为“分量”，分量为正值表示矢量分力的方向跟坐标轴的方向相同，分量为负值表示矢量分力的方向跟坐标轴的方向相反。

    第二点，确定矢量正交分量的坐标轴，不一定是取竖直方向和水平方向。例如，分析物体在斜面上的受力情况，一般选取X轴和斜面平行，Y轴和斜面垂直。坐标轴的选取是以使问题的分析简化为原则。通常选取坐标轴的方法是：选取一条坐标轴与物体运动的加速度的方向相同（包括处理物体在斜面上运动的问题），使得物体沿另一条坐标轴的加速度为零，这样就可得到外力在该坐标轴上的分量之和为零。