数字电路基础知识

    任务描述

    本任务是能根据输入信号的逻辑值分析出输出端的逻辑值，根据任务要求，需要电工班准备原材料，并检测其好坏，以便进行下一步的焊接。

    任务目标

    1.能进行数值之间的相互转化。

    2.能对逻辑代数进行计算。

    3.能正确描述基本门电路的基本性质和主要功能。

    4.能利用万用表检测门电路等元器件的好坏。

    5.会分析门电路的逻辑关系。

    6.能写出基本门电路的真值表。

    7.会分析74LS00集成块的逻辑关系。

    知识准备

    材料准备：万用表、与、或、非门电路、74LS00集成块。

    资讯准备：在数字电路中，经常需要检测出输出端的高低电压，来判断输出信号的逻辑关系，这需要会检测元件并掌握各门电路的逻辑关系。

    此外，还需要掌握以下相关理论：

    一、二进制代码

    码制：编制代码所要遵循的规则。

    二进制代码的位数（n）与需要编码的事件（或信息）的个数（N）之间应满足以下关系：N≤2n。

    1.二—十进制码

    概念：用4位二进制数来表示十进制数中的0~9十个数码，简称BCD码。

    从4 位二进制数16种代码中，选择10种来表示0~9个数码的方案有很多种，每种方案产生一种BCD码。

    （1）几种常用BCD代码（表6-1）

    表6-1     常用的BCD代码

    （2）各种编码的特点 有权码：编码与所表示的十进制数之间的转换关系，如（10010000） 8421BCD=（90）D；

    余3码的特点：当两个十进制的和是10时，相应的二进制正好是16，于是可自动产生进位信号，而不需修正。0和9，1和8，…，6和4的余3码互为反码，这对求10的补码很方便。

    余3码循环码：相邻的两个代码之间仅一位的状态不同。按余3码循环码组成计数器时，每次转换过程只有一个触发器翻转，译码时不会发生竞争－冒险现象。

    （3）用BCD代码表示十进制数 对于一个多位的十进制数，需要由与十进制位数相同的几组BCD代码来表示。例如：

    （4）求BCD代码表示的十进制数 对于有权BCD码，可以根据位权展开求得所代表的十进制数。例如：

    0111（8421 BCD）=0×8+1×4+1×2+1×1=（7）D

    二、二值逻辑变量与基本逻辑运算

    逻辑运算：当0和1表示逻辑状态时，两个二进制数码按照某种特定的因果关系进行的运算。逻辑运算使用的数学工具是逻辑代数。

    逻辑代数：与普通代数不同，逻辑代数中的变量只有0和1两个可取值，它们分别用来表示两个完全对立的逻辑状态。在逻辑代数中，有与、或、非三种基本的逻辑运算。

    逻辑运算的描述方式：逻辑代数表达式、真值表、逻辑图、卡诺图、波形图和硬件描述语言（HDL） 等。

    1.与逻辑

    定义：只有当决定一个事件的所有条件都成立时，事件才会发生。

    表示：Y=A·B。

    （1）运算规则

    0·0 = 0 1·0 = 0

    0·1 = 0 1·1 = 1

    开关控制和逻辑电路如图6-1所示。

    图6-1  开关控制与逻辑电路

    （2）与门的真值表（表6-2）

    表6-2 与门的真值表

    真值表：用1和0表示的所有可能的输入状态的取值和相应的输出状态的取值所组成的表格。

    与门的逻辑表达式为：Y=AB

    （3）与门逻辑符号（图6-2）

    图6-2  与门逻辑符号

    2.或逻辑

    定义：在决定一个事件发生的几个条件中，只要其中一个或者一个以上的条件成立，事件就会发生。

    表示：Y=A+B。

    开关控制或逻辑电路如图6-3所示。

    图6-3  开关控制或逻辑电路

    （1）运算规则

    0+0=0　 0+1=1

    1+0=1　 1+1=1

    （2）或门的真值表（表6-3）

    表6-3 或门的真值表

    （3）或门的逻辑符号（图6-4）

    图6-4  或门逻辑符号

    3.非逻辑

    定义：在事件中，结果总是和条件呈相反状态的逻辑关系。

    表示：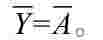

    （1）逻辑电路（图6-5）

    图6-5  开关控制或逻辑电路

    （2）非门电路的真值表（表6-4）

    表6-4 非门的真值表

    （3）非门的逻辑符号（图6-6）

    图6-6  非门逻辑符号

    4.复合逻辑门电路

    （1）与非运算 逻辑表达式为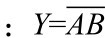。与非门的真值见表6-5，逻辑符号如图6-7所示。

    表6-5 与非门的真值表

    图6-7  与非门逻辑符号

    （2）或非运算 逻辑表达式为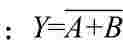。或非门的真值见表6-6，逻辑符号如图6-8所示。

    表6-6 或非门的真值表

    图6-8  或非门逻辑符号

    （3）异或运算 逻辑表达式为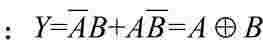。异或门的真值见表6-7、异或门逻辑符号如图6-9所示。

    表6-7 异或门的真值表

    图6-9  异或门逻辑符号

    （4）同或运算 逻辑表达式为：Y=A⊙B。同或门真值见表6-8、同或门逻辑符号如图6-10所示。

    表6-8 同或门的真值表

    图6-10  同或门逻辑符号

    （5）与或非运算 逻辑表达式为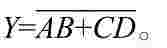：与或非门逻辑符号如图6-11所示，等效电路如图6-12所示。

    图6-11  与或非门逻辑符号

    图6-12  与或非门等效电路

    三、逻辑代数及其表示方法

    1.真值表表示方法

    图6-13所示为楼道灯开关电路图，其逻辑真值见表6-9。

    图6-13  楼道开关电路

    开关：变量 A、B；

    灯：函数L；

    A、B：向上为1，向下为0；

    L：亮–1；灭–0

    表6-9 逻辑真值表

    2.逻辑表达式表示方法

    逻辑表达式是用与、或、非等运算组合起来，表示逻辑函数与逻辑变量之间关系的逻辑代数式。

    例：已知某逻辑函数的真值表（表6-10），试写出对应的逻辑函数表达式。

    表6-10 逻辑真值表

    由表6-10真值表可得Y=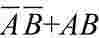

    3.逻辑图表示方法

    用与、或、非等逻辑符号表示逻辑函数中各变量之间的逻辑关系所得到的图形称为逻辑图。

    将逻辑函数式中所有的与、或、非运算符号用相应的逻辑符号代替，并按照逻辑运算的先后次序将这些逻辑符号连接起来，就得到与电路所对应的逻辑图。

    例：已知某逻辑函数表达式为：L=，试画出其逻辑图（图6-14）。

    图6-14  逻辑图

    4.波形图表示方法（图6-15）

    图6-15  时序图

    用输入端在不同逻辑信号作用下所对应的输出信号的波形图，表示电路的逻辑关系。

    例：通过下面真值表6-11画出波形图。

    表6-11 逻辑真值表

    四、逻辑代数

    1.逻辑代数的基本定律和恒等式

    （1）常量之间的关系

    与运算：0·0=0　 0·1=0　 1·0=0　 1·1=1

    或运算：0+0=0　 0+1=1　 1+0=1　 1+1=1

    非运算

    （2）基本公式

    0–1律：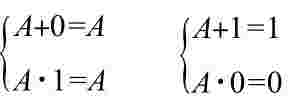

    互补律：

    等幂律：A+A=A　 A·A=A

    双重否定律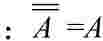

    分别令A=0及A=1代入这些公式，即可证明它们的正确性。

    （3）常用公式

    还原律：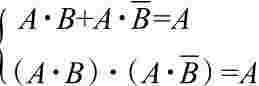

    吸收律：

    证明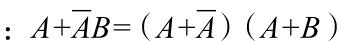

    =1·（A+B）

    =A+B

    分配律：A+BC=（A+B）（A+C）

    互补律：A+A=1

    冗余律：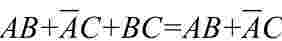

    2.逻辑代数的基本规则

    （1）代入规则 任何一个含有变量A的等式，如果将所有出现A的位置都用同一个逻辑函数代替，则等式仍然成立。这个规则称为代入规则。

    例如：已知等式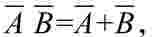用函数Y=AC代替等式中的A，根据代入规则，等式仍然成立，即有：

    （2）反演规则 对于任何一个逻辑表达式Y，如果将表达式中的所有“·”换成“＋”，“＋”换成“·”，“0”换成“1”，“1”换成“0”，原变量换成反变量，反变量换成原变量，那么所得到的表达式就是函数Y的反函数Y（或称补函数），这个规则称为反演规则。例如：

    Y=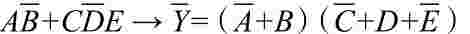

    Y=

    注意：运用反演规则应注意以下两个原则。

    ①保持原来的运算优先级，即先进行与运算，后进行或运算，并注意优先考虑括号内的运算。

    ②对于反变量以外的非号应保留不变。

    五、逻辑函数化简方法

    逻辑函数的公式化简法就是运用逻辑代数的基本公式、定理和规则来化简逻辑函数。

    1.并项法

    利用公式A+A=1，将两项合并为一项，并消去一个变量。

    例如：

    Y1=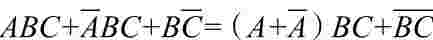

    =

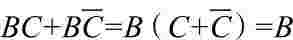
    Y2=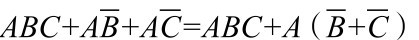

    =

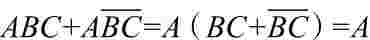
    2.吸收法

    （1）利用公式A+AB=A，消去多余的项。

    例如：

    Y1=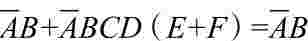

    Y2=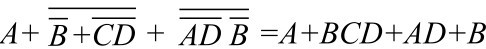

    =（A+AD）+（B+BCD）=A+B

    （2）利用公式A+AB=A+B，消去多余的变量。

    Y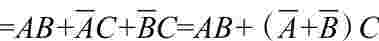

    =

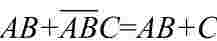
    Y=

    =

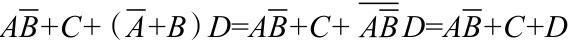
    3.配项法

    （1）利用公式A=A（B+B），为某一项配上其所缺的变量，以便用其他方法进行化简。

    Y=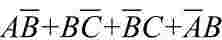

    =

    =

    =

    =

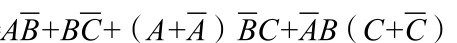
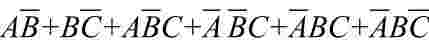
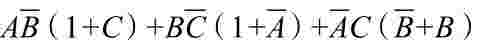
    （2）利用公式A+A=A，为某项配上其所能合并的项。

    Y=

    =

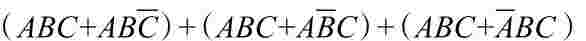
    =AB+AC+BC

    4.消去冗余项法

    利用冗余律AB+AC+BC=AB+AC，将冗余项BC消去。

    Y1=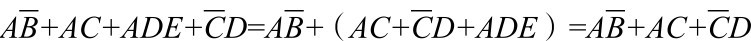

    Y2=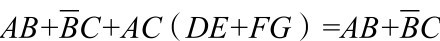

    六、由逻辑函数画出逻辑图

    一个逻辑函数的表达式可以有与或表达式、或与表达式、与非—与非表达式、或非—或非表达式、与或非表达式5种表示形式，每种表达式对应一个逻辑图。

    步骤：（1）根据文字要求将逻辑函数化成所需形式；

    （2）根据所得逻辑函数选择逻辑门，然后逐级画出逻辑图。

    例：已知逻辑函数表达式为：L=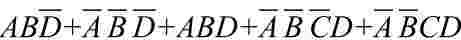

    （1）求最简的与或逻辑函数表达式，并画出相应的逻辑图；

    （2）仅用与非门画出最简表达式的逻辑图。

    解：

    L=

    =

    =

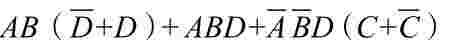
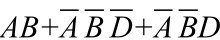
    =（与－或表达式）

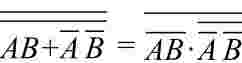    =（与非－与非表达式）

    根据最简与或表达式画逻辑图，如图6-16所示。

    图6-16  最简与或逻辑图

    根据最简与非－与非表达式画逻辑图，如图6-17所示。

    图6-17  最简与非逻辑图

    任务实施

    一、认知表决器电路图（图6-18）

    图6-18  表决器电路图

    在本次任务中采用正逻辑体制，评委同意为“1”，不同意为“0”，表决结果通过为“1”，不通过为“0”。

    二、列出元器件清单（表6-12）

    表6-12 元器件清单

    三、根据元件清单选择元器件

    1.二极管的选择。

    2.集成块的选择。

    3.电阻的选择。

    任务评价

    以小组为单位，选择演示文稿、展板、海报、录像等形式中的一种或几种，向全班展示汇报学习成果。

    综合评价表

    任务拓展

    一、74LS00的检测

    74LS00四组2输入端与非门（正逻辑），共有54/7400、54/74H00、54/74S00、54/74LS00四种。

    1.引脚图

    74LS00引脚如图6-19所示。

    图6-19  74LS00引脚图

    引脚说明：1A－4A，1B－4B 输入端，1Y－4Y 输出端，Vcc：电源，GND：地。

    2.功能表

    74LS00真值见表6-13。

    表6-13　74LS00真值表

    二、CD4012和2003构成的三人表决器

    图6-20  CD4012和2003构成的三人表决器

    任务检测

    一、画图题

    1.画出与、或、非门符号。

    2.画出以下门电路真值表。

    （1）与门　 （2）非门　 （3）或非门　 （4）与非门

    二、计算题

    （1 101 010）2=（ ）10　 （128）8=（ ）10

    三、简答题

    1.画出74LS00内部结构及引脚图。

    2.查阅相关资料，简述用万用表如何判别74LS00的好坏。