
为了弥补混合长假设的局限性,有一些紊流模型通过求解紊动量的微分输运方程来考虑紊动量的输运。这类模型发展中的重要一步,是放弃速度比尺和时均速度梯度之间的直接联系,转而根据微分输运方程确定速度比尺,构成一方程紊流模型——k方程模型。
5.9.1 紊动动能k方程模型
如果用一个比尺表征紊流速度脉动的特性,物理上最有意义的比尺是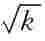 ,其中为(5-34)式定义的单位质量的紊动动能,是三个方向的紊流脉动强度的直接度量。动能k主要包含在大比尺紊动之中,故
,其中为(5-34)式定义的单位质量的紊动动能,是三个方向的紊流脉动强度的直接度量。动能k主要包含在大比尺紊动之中,故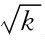 是大比尺紊动的速度比尺。
是大比尺紊动的速度比尺。
将 作为速度比尺
作为速度比尺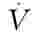 ,代入(5-35)式,可得
,代入(5-35)式,可得
式中Cμ′为经验常数。此式被称为柯莫哥洛夫-普朗特表达式,是由柯莫哥洛夫和普朗特独立地得出。他们还建议通过求解k的输运方程来确定k的分布。
在前面我们导出了紊动动能k的输运方程(5-31)。人们在紊流平均运动的连续性方程和动量方程的基础上,添加了一个紊动能方程以力图组成封闭方程组。一方程模型(k方程模型)的命名便由此得来。但是精确的k方程在紊流模型中无法使用,因为扩散项和耗散项中出现了新的未知的相关关系。为了得到封闭的方程组,必须提出假设,对这两项进行模拟。与标量扩散的表达式(5-37)相似,可假设k的扩散通量与k的梯度成正比,即
式中,σk为经验常数。
耗散项ε可用下式进行模拟,即
式中,CD亦为经验常数。
在第5.1节中我们已经说明,尽管耗散发生于最小的涡旋,但耗散率ε却由大比尺运动决定。既然k和L表征着大比尺运动的特性,由因次分析易得(5-46)式。
将(5-45)式、(5-46)式代入紊动动能方程(5-31),并对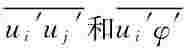 采用紊动黏性系数和紊动扩散系数表达式(5-32)和式(5-37),k方程可写为
采用紊动黏性系数和紊动扩散系数表达式(5-32)和式(5-37),k方程可写为
此式即是大多数单方程模型中采用的k的输运方程。其中经验常数的数值为Cμ′CD≈0.09, σk≈1。这里,对计算有意义的数值不是Cμ′和CD各自的数值,而是其乘积Cμ′CD;Cμ′和CD的各自的数值只是确定长度比尺L的绝对大小,并无重要意义。
这里介绍的紊流模型,只限于模拟高雷诺数水流,不能用于靠近壁面的黏性底层,因为方程(5-47)中略去了分子黏性扩散项。至于在求解k方程过程中,如何将微分方程对黏性底层积分,将在第5.12节中叙述。
5.9.2 混合长假设是紊动处于当地平衡的特例
在k方程(5-47)中,如果变化率项、对流输运项、扩散输运项均可忽略不计,则k的产生等于k的耗散,这样的紊动被称为处于当地平衡状态。对于无浮力的剪力层,k方程变为
将上式代入柯莫哥洛夫-普朗特表达式(5-44),消去k,可得
这正是方程(5-40)中引入的混合长公式,因为可将混合长lm视作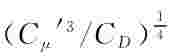 乘以长度比尺L。这一推导清楚地表明,混合长模型只适合于紊动处于当地平稳状态的水流。
乘以长度比尺L。这一推导清楚地表明,混合长模型只适合于紊动处于当地平稳状态的水流。
5.9.3 一方程模型的适用范围
一方程模型考虑到紊动速度比尺的对流输运和扩散输运;在非恒定流动中,还考虑到紊动的历史。当对流输运或扩散输运比较重要时,一方程模型自然比混合长模型优越得多。
但是,一方程模型中关于如何确定长度比尺L,目前仍为不易解决的问题。对于比剪力层复杂的流动,欲确定长度比尺的分布就如同在混合长模型中确定混合长的分布一样,很难用经验方法解决。这使得一方程模型迄今为止仍限用于剪力层流动。对于剪力层型的流动,前已述及,混合长模型也可得出满意的结果,且比一方程模型更为简单。
为了满足紊流模型发展的实际需要,人们转而开始寻求更普遍、更精细的方法来确定长度比尺L的分布,其结果就是二方程紊流模型。
上一篇:人力资源管理的概念与职能
下一篇:基因座与基因座间相关性分析





.jpg)
.jpg)
