
在单位脉冲激励下的振动响应,称为单位脉冲响应函数。由于理想的单位脉冲载荷的激励频率范围是无限的,作为单位脉冲激励下的响应,单位脉冲响应函数包含了振动系统的全部动力特征参数。运用杜哈梅尔(Duhamel)积分可以求出系统对于一般非周期动载荷激励下的振动响应。
(一)单位脉冲响应函数
单位脉冲函数定义为

并有
![]()
具有以上形式的函数称为δ函数,也称为单位脉冲函数。该函数具有许多非常重要的性质,在许多领域的数值分析中都起到相当大的作用。任何一函数x(t)与δ(t)相乘的积分值等于此函数在零点的函数值x(0),即
![]()
式中,c——常数。
(1)任一函数x(t)与具有时移的单位脉冲函数δ(t-t0)乘积的积分值是在该时移点上此函数的函数值x(t0),即
![]()
(2)任一函数x(t)与δ(t)的卷积仍是此函数本身,即
![]()
(3)单位脉冲函数的傅里叶变换等于1,即
![]()
这一特征表明,单位脉冲激振力的傅里叶变换与白噪声的傅里叶变换是相同的。这说明单位脉冲激振力是一种宽频带的激振力。
单位脉冲力作用于单自由度系统时,其振动微分方程为
![]()
对式(2-31)积分并取极限得

可解得

这说明单位脉冲激励使系统获得初始速度x·(0)=1/m。因为这一脉冲作用的时间很短,此后系统即作自由振动,并由下式:
![]()
以及初始条件t=0时,x(0)=0,x·(0)=1/m,可确定X和φ,最后将得到

其中,无阻尼固有频率为

阻尼比为

有阻尼固有频率为
![]()
在式(2-35)中,x(t)的表达式通常称为单位脉冲响应位移函数,一般用h(t)来表示,代入式(2-35)为
![]()
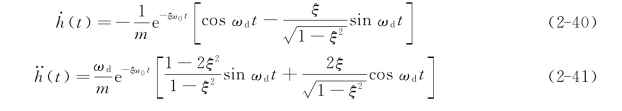
![]()
同理,单自由度系统在单位脉冲荷载作用下的速度和加速度反应分别为H(ω)直接反映系统固有的动力特征,即系统的固有频率、阻尼比等。也可以通过对频域响应函数H(ω)进行傅里叶逆变换,求出单位脉冲位移响应函数h(t)。
(三)杜哈梅尔积分
系统在脉冲函数作用下,其响应可表示为脉冲响应函数h(t)。若系统受到连续力函数f(t)的作用,其响应可用杜哈梅尔积分来求得。杜哈梅尔积分的基本原理是将力函数f(t)用一系列时间间隔为Δτ矩形脉冲函数来近似代替f(t)的作用,其响应可由这一系列脉冲响应的叠加得到
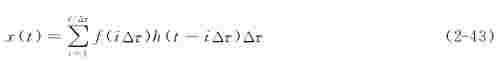
(二)单位脉冲响应函数的傅里叶变换
单位脉冲位移响应函数h(t)的傅里叶变换被称为频率响应函数,用H(ω)来表示,即
当Δτ足够小,Δτ→dτ,则上式的叠加可用积分形式代替,即
![]()





.jpg)
.jpg)
