
一、二重极限的概念及计算
1.二重极限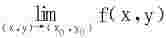 的ε-δ定义(方形邻域或圆形邻域)。
的ε-δ定义(方形邻域或圆形邻域)。
2.海因定理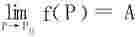 的充分必要条件是:P以任何点列、任何方式趋于P0时,f(P)的极限都是A。
的充分必要条件是:P以任何点列、任何方式趋于P0时,f(P)的极限都是A。
注 当动点P以不同方式或路径趋于P0时,f(P)的极限不相等,则可以判定二重极限不存在。
3.若两个累次极限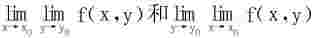 都存在但不等,则可以判定二重极限不存在。
都存在但不等,则可以判定二重极限不存在。
例1 利用ε-δ语言证明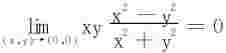 。
。
证一 显而易见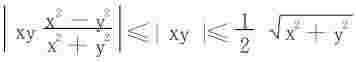
∀ε>0,若采用方形邻域,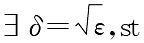
当|x|<δ,|y|<δ,且x2+y2≠0时,必有|f(x,y)-0|<ε。
若采用圆形邻域,∃δ=2ε,st
当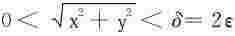 时,有|f(x,y)-0|<ε,证得
时,有|f(x,y)-0|<ε,证得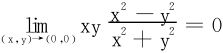 。
。
证二 利用极坐标变换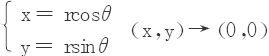 等价于r→0
等价于r→0

∀ε>0,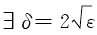 ,当0<r<δ时,有|f(x,y)-0|<ε成立。
,当0<r<δ时,有|f(x,y)-0|<ε成立。
例2 讨论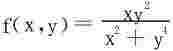 在原点处的极限。
在原点处的极限。
解 尝试P(x,y)沿着不同路径趋于原点时的极限
沿直线L:y=kx趋于(0,0)时,易知
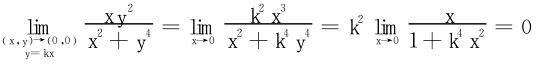
沿抛物线C:x=y2趋于(0,0)时
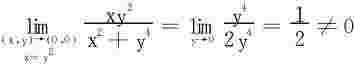
所以二重极限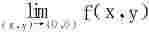 不存在。再讨论一下两个累次极限,易知
不存在。再讨论一下两个累次极限,易知
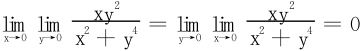
例3 求下列极限
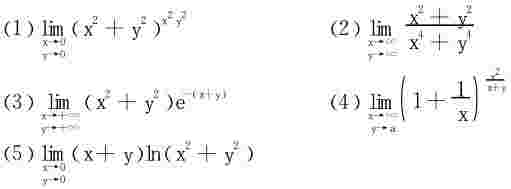
解 (1)取对数 记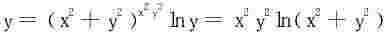
利用极坐标变换lny=r4cos2θsin2θlnr2
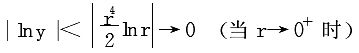
故原极限=e0=1

或利用极坐标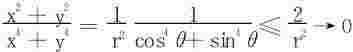
(3)对于充分大的x和y
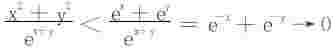
或x2+y2<(x+y)2,(x>0,y>0)
令x+y=u
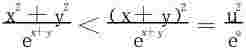
u→+∞时,上式趋于0。
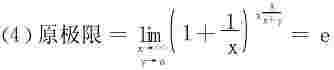
(5)利用极坐标变换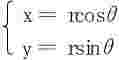
|(x+y)ln(x2+y2)|=r|cosθ+sinθ||lnr2|<4r|lnr|→0
或利用不等式: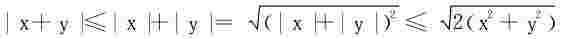
二、累次极限以及与二重极限的相互关系
1.累次极限的概念
2.累次极限面面观
(1)两个累次极限存在且相等,如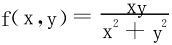 在P0(0,0)处;
在P0(0,0)处;
(2)两个累次极限存在但不相等,如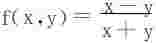 在P0(0,0)处;
在P0(0,0)处;
(3)仅一个累次极限存在,如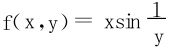 在P0(0,0)处;
在P0(0,0)处;
(4)两个累次极限都不存在,如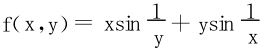 在P0(0,0)处。
在P0(0,0)处。
3.累次极限和二重极限之关系
(1)两个累次极限存在且相等,重极限未必存在,如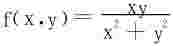 在P0(0,0)处;
在P0(0,0)处;
(2)重极限存在,累次极限可以不存在,如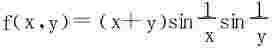 在P0(0,0)处;
在P0(0,0)处;
(3)若已知重极限和某个累次极限存在,则两者一定相等。
(4)若f在P0的两个累次极限皆存在但不等,则二重极限一定不存在。
例4 讨论下列函数在(0,0)的重极限与累次极限

解 (1)易知两个累次极限皆等于0,下面考虑二重极限。若二重极限存在的话,其值一定等于0;但在直线L:y=-x上,f(x,y)没有定义,故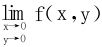 不存在。
不存在。
以极坐标变换解之:
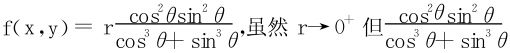 未必有界,亦得知二重极限不存在。
未必有界,亦得知二重极限不存在。
注 若限制动点P(x,y)在第一象限范围趋于(0,0),则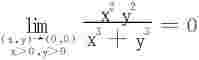 存在。
存在。
(2)∀y≠0,先考虑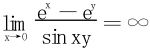 ,知累次极限
,知累次极限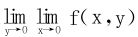 不存在,类似地,另一个累次极限亦不存在。再讨论二重极限。
不存在,类似地,另一个累次极限亦不存在。再讨论二重极限。
沿着直线L:y=2x趋于(0,0)时,
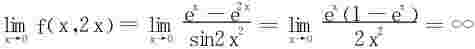
得知二重极限也不存在。
三、连续性
1.定义 设f为定义在平面点集D⊂R2上的二元函数,P0∈D,若∀ε>0,∃δ>0,只要P∈U(P0,δ)∩D,就有
|f(P)-f(P0)|<ε
则称f关于集合D在点P0连续。若f在D上任何点都连续,称f为D上连续函数。
注1.通常D为平面区域(开区域,闭区域,及一般区域)。
当P0是D的边界点时,上述定义中的P∈U(P0,δ)∩D就显得必不可少。
2.有界闭区域上连续函数的性质。(类似一元函数)
3.连续函数的复合函数的连续性。(复合运算的保连续性)
例5 研究下列函数的连续性
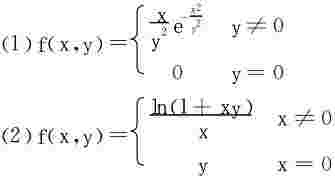
解 (1)只要讨论f在x轴上的连续性,∀x0≠0,在(x0,0)点
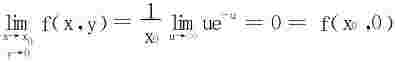
知f(x,y)在点(x0,0)处连续。在(0,0)点沿L:y=x趋于(0,0)时,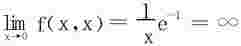 不存在极限,函数仅在原点(0,0)有间断。
不存在极限,函数仅在原点(0,0)有间断。
(2)函数的定义域是
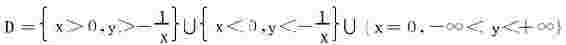
只要考虑其在y轴上的连续性。
∀y轴上的点P0(0,y0)处,当(x,y)→(0,y0)时,xy→0,利用等价无穷小量ln(1+u)~u (u→0),得知

于是f(x,y)在y轴上处处连续,而在定义域的其他点处连续性显见,总之f在定义域内处处连续。
例6 根据下面的每一个条件证明f(x,y)在区域G连续。
(1)f(x,y)在区域G内对x连续,且对y满足Lipschitz条件
|f(x,y′)-f(x,y″)|≤L|y′-y″|
其中(x,y′,(x,y″)∈G,L为常数。
(2)f(x,y)在G内对x连续,且关于x对y一致连续。
(3)f(x,y)对x和y分别连续,并对其中一个单调。
证明 (1)∀P0(x0,y0)∈G,分析
|f(x,y)-f(x0,y0)|≤L|f(x,y)-f(x,y0)|+|f(x,y0)-f(x0,y0)|
∀ε>0,由于f(x,y0)是x的连续函数,∃δ1>0,当|x-x0|<δ1时,
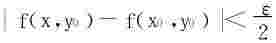
又由Lipschitz条件,取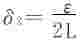 ,当|y-y0|<δ2时,
,当|y-y0|<δ2时,
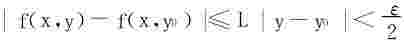 ,∀x∈U(x0;δ1)成立。
,∀x∈U(x0;δ1)成立。
于是取δ=min{δ1,δ2},当|x-x0|<δ,|y-y0|<δ时,有
|f(x,y)-f(x0,y0)|<ε
证得f在G内处处连续。
(2)和(1)类似,关键在于对条件“f(x,y)关于x对y一致连续”的理解:
∀ε>0,∃δ>0,当|y-y0|<δ时,有
|f(x,y)-f(x,y0)|<ε
∀x成立,即δ对于所有的x是一致通用的!!
(3)设f对x单调增加,∀ε>0,首先∃δ1>0,st|x-x0|≤δ1时,
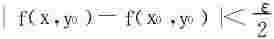
又f(x0±δ1,y)关于y连续,∃δ2>0,当|y-y0|<δ2时,有
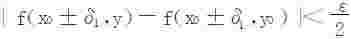
故当|x-x0|≤δ1,|y-y0|<δ2时,有
综合之:
|f(x,y)-f(x0,y0)|<ε
所以 f(x,y)在G中任一点(x0,y0)处连续。证毕。
注 二元函数f(x,y)关于两个单变量分别连续(甚至可偏导)时,并不能推得二元连续,如
例7 设f在单位元上有定义,f(x,0)在x=0连续,且fy′在G上有界,则f在(0,0)连续。
(北京大学98年)
证明 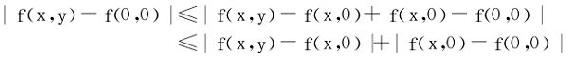
上一篇:内源性代谢途径
下一篇:各类农村金融机构及业务特点





.jpg)
.jpg)
