膜式水冷壁的管壁及鳍片温度

    14.1.3　膜式水冷壁的管壁及鳍片温度

    

    

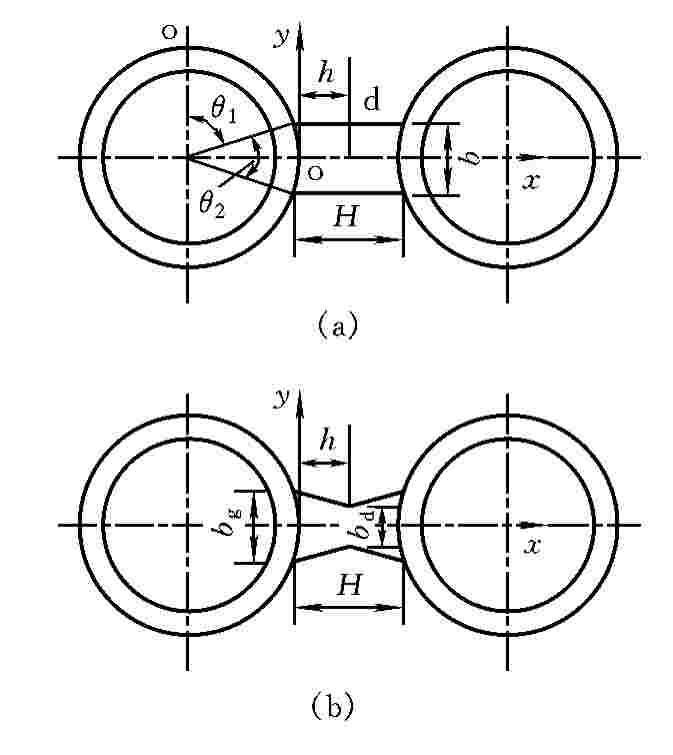
    图14.5　对称鳍片管结构图

    （a）矩形鳍片管；（b）梯形鳍片管

    膜式水冷壁广泛应用于高参数、大容量锅炉，其鳍片结构型式一般分为两种，将扁钢焊接在两管之间的矩形鳍片和与管子一起制造成型的梯形鳍片，如图14.5所示。膜式水冷壁的最高壁温可能出现在管子向火面的o点上，也可能出现在鳍片端部的d点处，这与热负荷q的分布规律、鳍片的形状尺寸、材料的导热系数λ和管内放热系数α₂等因素有关。一般情况下，其它条件相同时，提高热负荷q，管子o点及鳍端d点的温度都升高，但鳍端温度上升更快。增大放热系数α₂，管子o点及鳍端d点的温度都降低，但管子o点温度降低更快。增加鳍片高度h，则鳍端d点的温度升高。

    因此，为了保证膜式水冷壁的可靠运行，分别要对管子向火正面点和鳍片端部这两点温度进行校核。管壁的校核要求壁温低于材料强度允许的温度，而鳍片端部温度的校核则是为了确定合适的鳍片结构尺寸，保证不会因鳍片温度过高引起材料的氧化，以及鳍片温差太大产生的热应力使得膜式水冷壁变形和焊缝开裂，从而影响锅炉运行的安全性。

    各种计算表明，由鳍片吸收，再通过鳍根传递给管子的热量对管子最高壁温点温度的影响小于4%，所以管子向火面o点温度的确定与光管的计算方法相同，其热量分流系数也可按14.1.2节方法确定。

    鳍片管温度场的分布规律也可用拉普拉斯导热方程进行理论求解^［2］。求解时认为，相邻两管及两管之间的结构参数、热力参数以及流动参数是完全对称的状况，通常符合锅炉蒸发受热面的情况。这里只介绍最简单的矩形结构鳍片温度场的求解方法，如图14.5（a）所示。求解时分为两个部分，对于图中θ₁区的圆管部分，其解和工程应用方法与14.1.2节所述情况完全相同。

    矩形鳍片部分的求解需做如下假定：①管内放热系数α₂及金属导热系数λ为常数；②沿管子长度方向无热量传递；③相邻两管的对称界面无热流通过；④通过背墙保温材料的散热量忽略不计；⑤鳍片吸收的热量均匀通过鳍根传递给管子；⑥鳍片的热负荷q（x）为常数，即不考虑q沿x方向的变化。这样，在直角坐标系下表示的拉普拉斯导热定解问题为

    

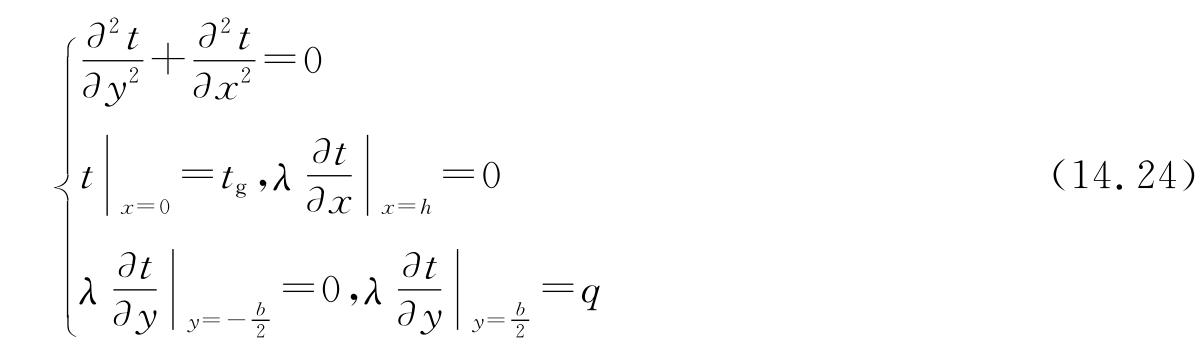
    对于上式表述的矩形鳍片边值问题，可采用分离变量法直接求得鳍端温度

    

    对于图14.5（b）中的梯形鳍片，与式（14.24）描述的矩形鳍片问题的差别主要是y坐标上的边界条件不同，其梯形边界曲线为y＝f（x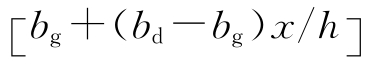）＝±/2，问题非常复杂，直接求解很困难。该问题的求解需要借助于复变函数的保角映射，通过变换将鳍片梯形区域变为平面的矩形区域，在进一步简化基础上，求得梯形鳍片的鰭端温度

    

    

    以上各式中：t_d和t_g分别为鳍端温度和鳍根温度，℃；b、b_d及b_g分别为鳍片厚度、鳍端厚度及鳍根厚度，m；h为鳍片高度，m；A为鳍片的形状系数，按式（14.27）确定或图14.6查取^［3］；a＝b_d/b_g，当a＝1，鳍端与鳍根的厚度相等时，式（14.26）变为矩形鳍片公式（14.25）。

    

    

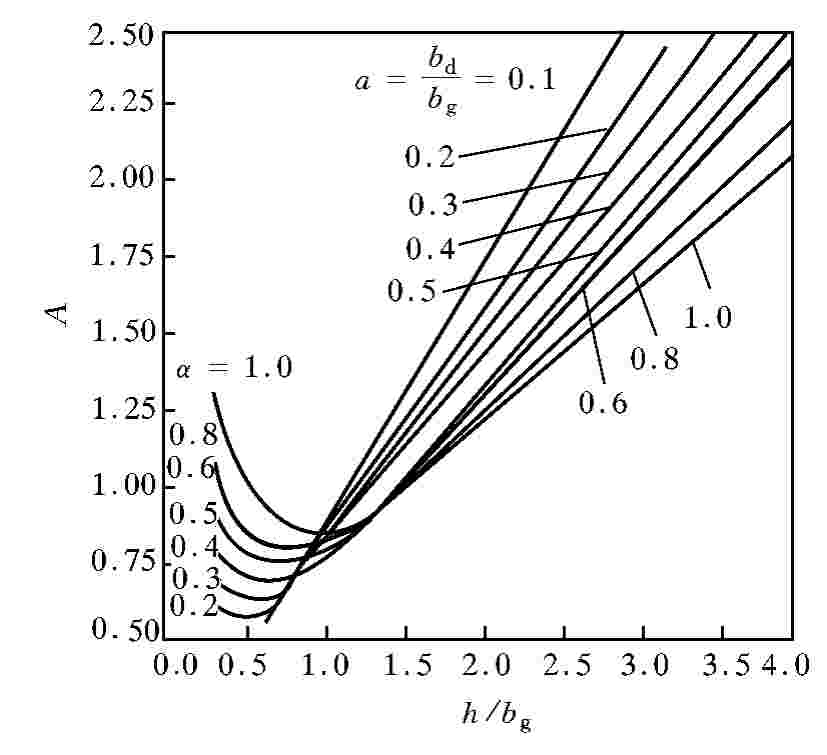
    图14.6　鳍片的形状系数A

    上述求解过程做了一些假定和简化，其结果是近似值，但对工程应用已有足够的精度。当然，得到更精确的结果也是可能的。

    由鳍片形状系数A的线算图14.6可以看出，当a值，即鳍片厚度的形状及尺寸一定时，存在一个鳍片高度h与厚度b_g的最佳比值，使得A有一极小值，此时鳍端温度最小。当h/b_g大于曲线中A的极小值所对应的h/b_g值后，随着a值的增大，即鳍端厚度增加或鳍根厚度减小，都使A值减小，则鳍端温度减小。这表明当鳍片高度增加后，为了使鳍端区域的热量尽快向管子传递，应当相应增加鳍端的厚度，最好采用矩形鳍片。而在h/b_g小于曲线中A的极小值所对应的h/b_g值范围，随着a值的减小，即减小鳍端厚度或增加鳍根厚度能使A值减小，从而降低鳍端的温度。因为这时的鳍片高度比较小，增加鳍根的厚度能加快鳍片吸收的热量向管子传递的速度，则最好采用梯形鳍片。

    

    

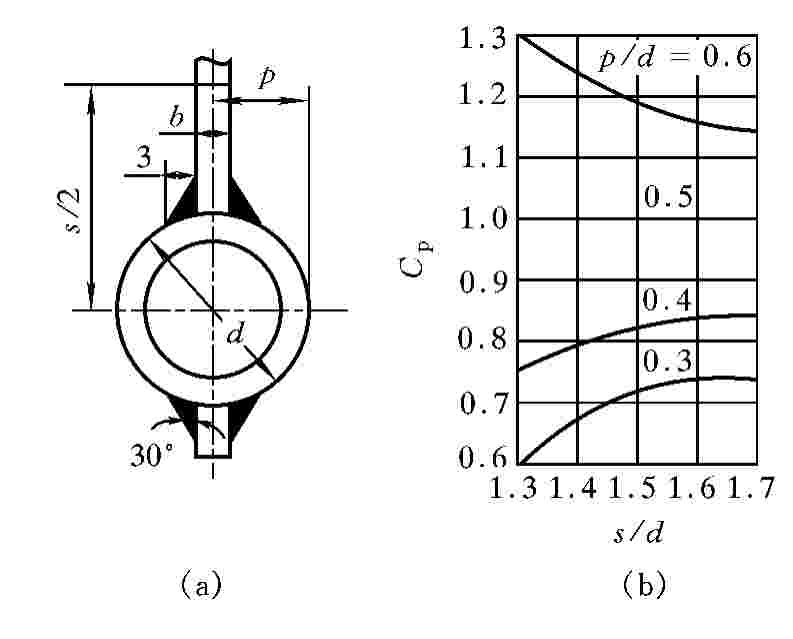
    图14.7　鳍片位置以及偏移修正系数C_p^［3］

    （a）鳍片位置；（b）偏移修正系数C_p

    锅炉通常采用的是将矩形扁钢焊在光管上制造成膜式水冷壁。鳍片的断面在近端部处呈矩形，而近根部处呈梯形，见图14.7（a）所示。焊接后的梯形横断面实际上增大了热量由鳍片向管子传递的面积，减小传热热阻，则降低了鰭端的温度。这种类型的鳍片温度场也可用精确方法求解，通过计算后得到修正焊缝影响的系数

    

    显然，K_hf＜1。

    实际上，鳍片热负荷q（x）的分布仍然存在不均匀性。同样，也可用前述热量分流系数的方法对q（x）进行修正。考虑了焊缝及热负荷不均匀性的影响后，鳍端温度的计算式由式（14.26）改写成

    

    式中：K_hf为焊缝修正系数，按手册或标准中的线算图查取；μd为鳍端热量分流系数，按手册或标准中的线算图查取。

    鳍根温度也是圆管上相应位置的温度，也采用鳍根热量分流系数的方法对均匀受热圆管的计算公式（14.19）进行修正，即

    

    式中：μ_g为鳍根分流系数，由下式确定

    

    式中：k_Bi、k_s及k_β为修正系数，按手册或标准中的线算图查取；C_p为考虑p/d≠0.5时鳍片位置偏移修正系数，按图14.7（b）^［3］查取。

    当火焰黑度0.5≤a_hy≤0.75时，应考虑从管子向鳍片的再辐射对鳍根温度和鳍端温度的影响。经过计算，与不考虑再辐射情况时相比，热量分流系数和鳍端温度均有所提高，此时，式（14.29）中的μ_d和式（14.30）中的μ_g均应乘以系数1.1。

    确定鳍片管强度时的计算温度，既非管子内外壁的平均温度，也不是图14.5中管子正面o点和鰭端d点的平均温度，而是鳍片管的积分平均温度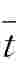，即管壁和鳍片截面各自积分平均温度的面积加权平均值，可近似地按下式计算：

    

    式中：F_g，F_q分别为管壁和鳍片的截面积，m²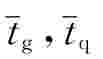分别为管壁和鳍片截面的积分平均温度，℃，按以下三式计算。

    管壁截面的积分平均温度为

    

    式中：x＝q_pj/q_max为相对平均热负荷。对于热力及几何对称的鳍片管，x＝s/πd，s为管间节距。

    矩形鳍片截面的积分平均温度为

    

    梯形鳍片截面的积分平均温度为

    

    式中：t_g为鳍根温度，℃，按式（14.30）确定；M为修正系数，按手册或标准中的线算图查取；a₀为平均照射系数，按手册或标准中的线算图查取。

    上面介绍的计算公式仅限于单面受辐射加热、几何条件和热力条件对称的膜式壁水冷壁的计算。其它结构及工况条件的计算可查阅有关锅炉手册及标准。