
引理3.1 对于任意t≥0,有
证明:设X(i)为总体1次SRS样本X1,X2,…,Xm中次序为i的样本单元,则X(i)的生存函数为S(i),i=1,2,…,m.令
则
那么
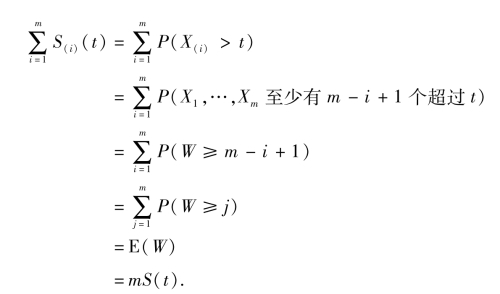
引理得证.
由引理3.1可以推出
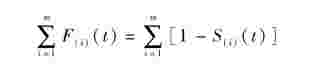
定理3.1 对于任意t≥0,有
![]()
证明:因为对于任意给定的i(i≤i≤m),X(i)1,X(i)2,…,X(i)k独立同分布,所以
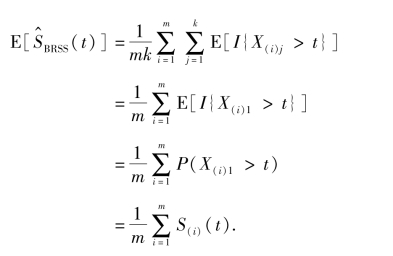
再由引理3.1即可得证.
定理3.2 对于任意t≥0,有
证明:由X(i)j,i=1,2,…,m;j=1,2,…,k的独立性和X(i)1,X(i)2,…X(i)k的独立同分布性,i=1,2,…,m,得
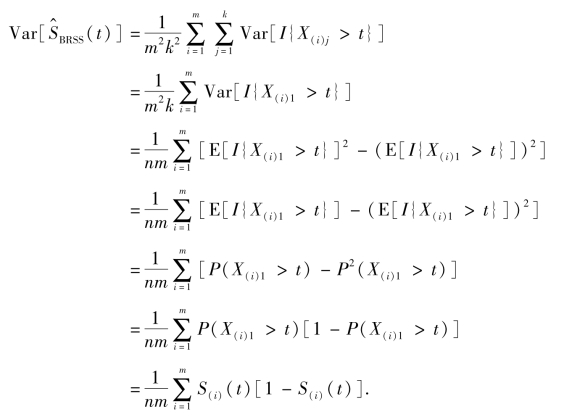
定理得证.
引理3.2[131](林德贝格-勒维中心极限定理)设{Zn}是独立同分布的随机变量序列,且E(Zi)=μ,Var(Zi)=σ2>0.记
则对任意实数y,有
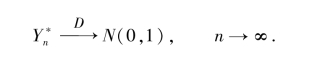
下面定理说明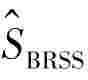 (t)具有渐近正态性.
(t)具有渐近正态性.
定理3.3 对于任意t≥0和给定的小组数m,有
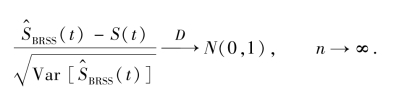
证明:令
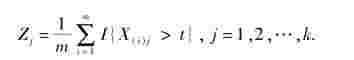
则由公式(3.6)知
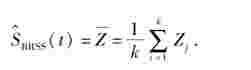
显然,Z1,Z2,…,Zk是独立同分布的,且
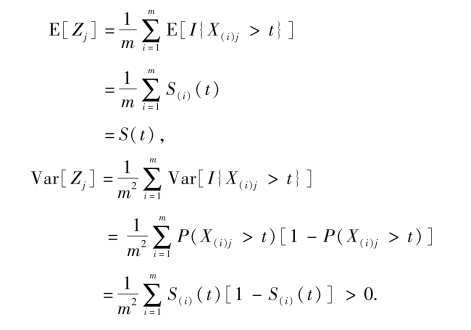
这样,由引理3.2得
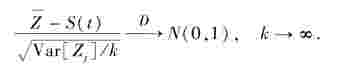
由定理3.2知
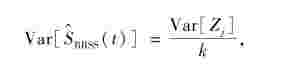
且k→∞与n→∞等价,于是定理得证.
这样,由定理3.3得,生存函数S(t)的置信水平1-α的置信区间为
其中uα/2为标准正态分布的上α/2分位数.
当n较大时,置信区间中Var[ (t)]可用
(t)]可用
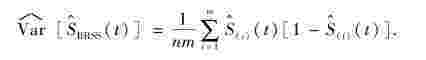
来代替,其中
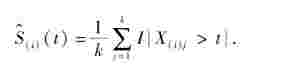





.jpg)
.jpg)
