与斯特列尔准则

    14.4　基于点扩散函数的空域像质评价方法（中心点亮度）与斯特列尔准则

    光学系统成像过程可以用图14.24的变换来表示，被成像物体通过一定的光学系统成像并输出图像。光学成像系统是成像过程中的核心变换环节，被成像物体即物的空间分布函数可视为系统的输入g_in（r），最后得到的可视图像即像的空间分布函数可视为系统的输出g_in（r），其中，r分别表示物、像的位置坐标矢量。以这种变换的观点可以描述系统的特性，并分析、比较、评价不同的成像系统。点扩散函数的空域像质评价方法就是基于点基元观点，运用光学衍射理论来研究光学系统输入与输出之间成像特性的。

    

    

    图14.24　光学系统成像过程

    光学系统的输入即物体可以看成是由无数具有不同光强度的发光点的集合，这些发光点经光学系统成像后在像面分别形成一定照度分布的衍射光斑像，它们叠加组合后即为系统输出的像，即整个像面的光强分布是由物面上各发光点在像面上所形成的光斑的叠加的结果。而衍射光斑像的照度分布规律（即点扩散函数）是由系统固有的剩余像差决定，反映了系统的成像特性，因此可用点扩散函数来评价系统的像质。

    为分析研究方便，可以将光学系统理想化为一线性平移不变系统，或称为空间不变线性系统。

    线性系统的基本含义是：多个信号和的输入，其输出是这些信号的输出之和。若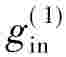（r）的输入信号产生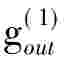（r）的输出信号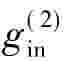，（r）的输入信号产生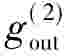（r）输出信号，则当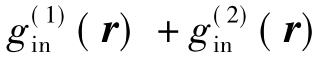为输入信号时，输出信号应为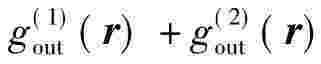，即线性叠加原理。线性系统的理论是一种强有力的分析工具，其优点在于，对任一个复杂的输入函数的响应，能用输入函数分解成的许多“基元”激励函数的响应表示出来。对有些非线性系统，可将问题分别考虑或加以修正，作一些近似的线性化处理。以下讨论将主要以线性系统理论为基础，并应用于光学成像系统。

    平移不变性或称空间不变性是指当输入信号作坐标平移即其输入位置变化时，其输出信号形式不变，只是同时平移一坐标值，即输出信号的位置变化。如当输入信号为g_in（r+Δr）时，则输出信号为g_out（r+Δr）。光学系统与之对应的特性是，当具有同一光强分布的物位于物面上不同位置时，其在像面上对应位置处将形成相同光强分布的像，即像与像之间除位置不同外，其光强分布的形状将是相同的。光学系统的这一特性常称为渐晕不变。对实际系统，只在一定小的区域范围内满足平移不变性，这样的范围称为等晕区。

    对于线性成像系统的任何输入函数都可以看成函数（点物）的叠加，即

    g_in（r）=∫dr＇g_in（r＇）δ（r－r＇）　　　　　　　　　　（14.22）

    对于二维图像，r、r＇为二维坐标矢量。式（14.22）右边g_in（r＇）可视为函数δ（r－r＇）的权重因子。按照线性系统的叠加原理，为了得到系统输入g_in（r）的输出g_out（r），只要知道系统对所有的δ（r－r＇）的输出即可。设系统对δ（r－r＇）的输出为h（r，r＇），则系统的输出g_out（r）可视为h（r，r＇）带权重g_in（r）的叠加，即

    g_out（r）=∫dr＇g_in（r＇）h（r，r＇）　　　　　　　　　　（14.23）

    一般说来h（r，r＇）依赖于输入δ函数的位置r＇。但是，对于平移不变成像系统，则h（r，r＇）将演变为h（r－r＇）形式，即h（r，r＇）的分布或形状不再依赖于r＇，因此式（14.24）可以简化为如下的卷积形式：

    g_out（r）=∫dr＇g_in（r＇）h（r－r＇）=g_in（r）＊＊h（r）　　　（14.24）

    式（14.24）说明对于线性平移不变系统，其输出g_out（r）是输入g_in（r）与函数h（r）的卷积。所以，用函数h（r）完全可以表征系统的行为和特性。光学成像系统中，h（r）的意义是点元物体的像，即系统的强度脉冲响应函数，也称为系统的点扩散函数。式（14.24）的物理意义是：光学线性平移不变系统，其像面上的强度分布是物面上强度分布与点扩散函数的卷积。因此，对任一成像系统，只要确定了其点扩散函数，就可以根据式（14.24）确定对应于任意输入信号的输出，即系统的成像特性可由点扩散函数反映出来。这里需要说明的是，实际上点扩散函数只能在有限物空间等晕区内保持平移不变。

    为了研究光学系统的点扩散函数h（r）与成像质量之间的关系，现用波动理论来分析点物即点基元δ（r）经过光学系统后的响应即在像面上的光波的振幅U（r）或光强分布h（r）。

    对于一个无像差光学系统，轴上物点在系统出瞳处的输出波阵面应是一个会聚球面波，如图14.25所示。图中，（ξ，η，ζ）为出瞳面坐标，（x，y，z）为像坐标，且轴ξ和轴X重合。根据惠更斯－菲涅尔原理，光学系统像点O附近P点的三维光场复振幅分布是

    

    

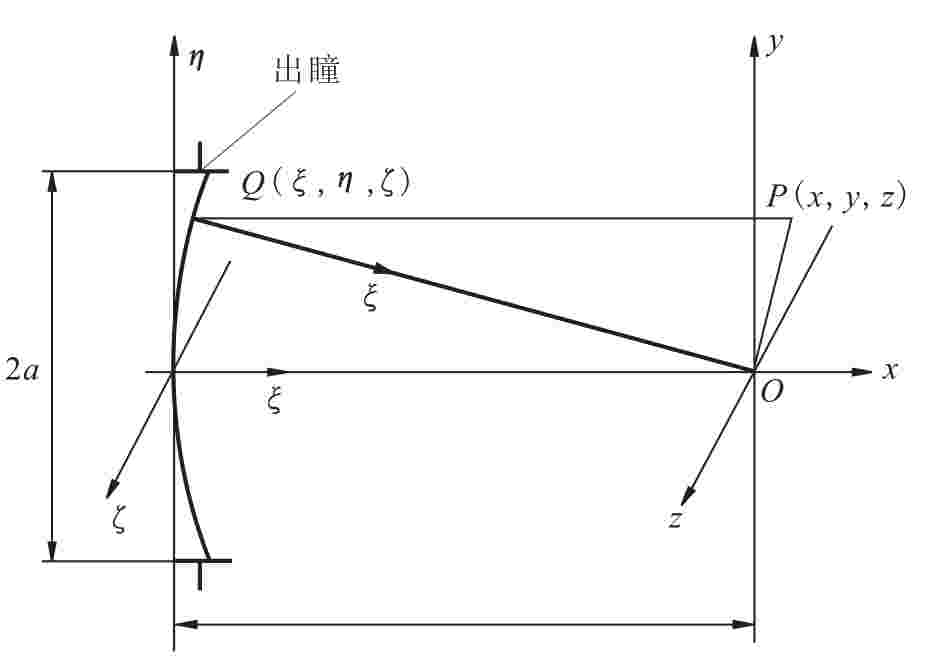
    图14.25　会聚球面波在圆孔上的衍射

    

    式中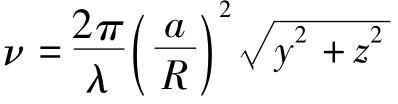，，a为出瞳半径，R为参考球面半径。P点坐标为

    （x，y，z），J₀（νρ）为第一类零阶贝赛尔函数。对应的高斯像面上的归一化光强度分布即点扩散函数，可由式（14.25）得到

    

    式（14.26）为像面上圆孔夫朗和费衍射图样的爱里斑光强分布公式。

    当光学系统存在像差时，根据惠更斯－菲涅尔原理，焦点O附近P点三维光场分布是

    

    式中：W（ρ，θ）——波像差，即实际波阵面相对于高斯波阵面的偏差，亦即图14.26中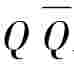之间的光程差；

    　　　（ρ，θ）——光瞳平面极坐标；

    　　　θ——以高斯像点为中心的极坐标的幅角。

    

    

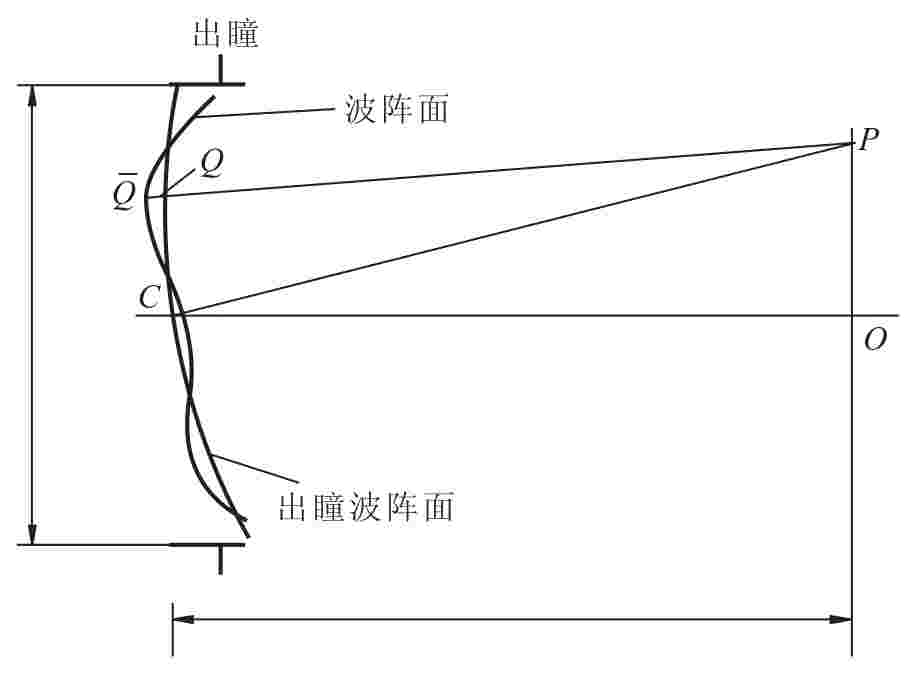
    图14.26　参考系与记号的选择

    若以无像差时的高斯像点处的光强度（式（14.26）的平方）来归一化光学系统存在像差时光强分布，则P点的归化强度为

    

    此即有像差时的点扩散函数。

    对于无像差的系统，高斯像面上的像点中心拥有最大的光强度；而当存在像差时，像点光强度分布将发生变化，中心极大光强将降低，光能量将向周围扩散。对于小像差系统，最大光强中心点的位置可以通过给波前函数附加少量的倾斜和离焦量以使得波前差的方差变得最小来获得。

    1894年，斯特列尔（K.Strehl）根据光学系统像差对点扩散函数中心点亮度的影响，提出了一个判断光学系统成像质量的指标，即用有像差时的点衍射图形中最大亮度与无像差时的最大亮度之比来表示光学系统成像质量（由式（14.29）定义），该比值即式（14.28）中时的归化值，被称为斯特列尔比（S.D），又称为中心点亮度。

    

    式中，W以波长为单位，它是相对于参考球面波的波像差。在像差不大时，中心点亮度和像差有较简单的关系，利用这种关系和上述判断就可以决定像差的最佳校正方案及像差公差。

    当波像差很小时，如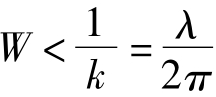，则式（14.29）中的被积函数可以展开成泰勒级数，则式（14.29）演变为

    

    如果像差做足够小，使得W的3次和更高次的幂的项可以被忽略，则上式可以化简为：

    S.D=1－（kΔw）²（14.31）

    式中，Δw为波像差方差，即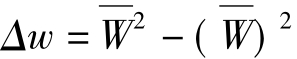，式中：

    

    因此，对于小像差系统，斯特列尔比与像差无关，其大小和波前畸变的方差成一定比例。

    式（14.31）适用于斯特列尔比大于0.5左右的情况。实用中，实际的斯特列尔比总是会比用这一公式估算出的结果要小。而下面的估算公式则适合大部分的像差类型：

    

    该公式适用于S.D＞0.1的情形。

    斯特列尔比是像质评价的一种数值判据方法，斯特列尔比与波面像差峰谷值（PV）和均方根值（RMS）有关。对于系统满足瑞利判据条件时，即PV＜λ/4时，S.D＞0.8。瑞利判据中有特征意义的是波面像差的峰谷值，但不严密，因为它没有考虑波面上的缺陷部分在整个面积中所占的比例。如占整个波面面积很小的缺陷却能可能引起很大的局部波像差，这按严格的瑞利判据是不允许的，但实际对成像并无明显影响；而大面积的小值波像差，却可能引起像质的严重下降。1947年Marechal研究波面像差均方根值与斯特列尔比关系时指出：当一个系统衍射焦点的归一化光强（即S.D）大于等于0.8时，就可以认为系统已经被很好地校正，其相应的RMS波像差为≤λ/14，此即Marechal判据。