
§7.4 幂级数及其和函数
幂级数及其收敛半径
形如
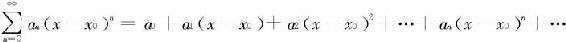 的级数称为幂级数,其中{an}是一数列,x视为变量,x0为一常数。为简单起见我们着重讨论x0=0的情况,即
的级数称为幂级数,其中{an}是一数列,x视为变量,x0为一常数。为简单起见我们着重讨论x0=0的情况,即
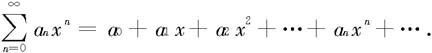
对于x0≠0情形,可通过平移变换x′=x-x0化成上述情形。
首先讨论幂级数的收敛性问题,对任何幂级数 来说,它在x=0处总是收敛的。对常数x0,若数项级数
来说,它在x=0处总是收敛的。对常数x0,若数项级数 收敛,则称幂级数
收敛,则称幂级数 在x0处收敛。此时也称x0为该幂级数的收敛点。否则,则称该幂级数在x0处发散。对于其他x的收敛状况,我们有如下重要定理。
在x0处收敛。此时也称x0为该幂级数的收敛点。否则,则称该幂级数在x0处发散。对于其他x的收敛状况,我们有如下重要定理。
定理7.4.1(Abel定理) 如果幂级数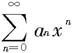 当x=x0≠0时收敛,则对于适合不等式|x|<|x0|的一切x,幂级数在x处绝对收敛;如果幂级数
当x=x0≠0时收敛,则对于适合不等式|x|<|x0|的一切x,幂级数在x处绝对收敛;如果幂级数 当x=x0时发散,则对于适合不等式|x|>|x0|的一切x,幂级数在x处发散。
当x=x0时发散,则对于适合不等式|x|>|x0|的一切x,幂级数在x处发散。
证明 先设x0是幂级数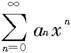 的收敛点,即级数
的收敛点,即级数
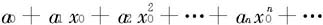
收敛。根据级数收敛的必要条件,这时有
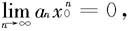
于是存在一个常数M,使得
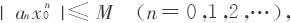
这样级数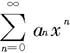 的一般项的绝对值
的一般项的绝对值
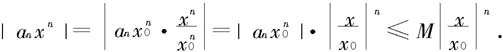
因为当|x|<|x0|时,等比级数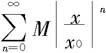 收敛,所以级数
收敛,所以级数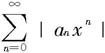 收敛,也就是级数
收敛,也就是级数 绝对收敛。
绝对收敛。
定理的第二部分可用反证法证明。倘若幂级数当x=x0时发散而有一个点x1适合|x1|>|x0|使级数收敛,则根据本定理的第一部分,级数当x=x0时应收敛,这与所设矛盾。定理得证。 □
定理7.4.1告诉我们,如果幂级数在x=x0处收敛,则对于开区间(-|x0|,|x0|)内的任何x,幂级数都收敛;如果幂级数在x=x0处发散,则对于闭区间[-|x0|,|x0|]外任何x,幂级数都发散。
推论7.4.2 如果幂级数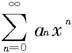 不是仅在x=0一点收敛,也不是在整个数轴上收敛,则必有一个完全确定的正数R存在,使得
不是仅在x=0一点收敛,也不是在整个数轴上收敛,则必有一个完全确定的正数R存在,使得
当|x|<R时,幂级数绝对收敛;
当|x|>R时,幂级数发散;
当x=R与x=-R时,幂级数可能收敛也可能发散。
正数R通常叫做幂级数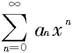 的收敛半径。由幂级数在x=±R处的收敛性就可以决定它在区间(-R,R),[-R,R),(-R,R]或[-R,R]上收敛,这区间叫做幂级数
的收敛半径。由幂级数在x=±R处的收敛性就可以决定它在区间(-R,R),[-R,R),(-R,R]或[-R,R]上收敛,这区间叫做幂级数 的收敛区间。
的收敛区间。
如果幂级数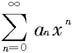 只在x=0处收敛,这时收敛域(即收敛点全体)只有一点x=0.但为了方便起见,我们规定这时收敛半径R=0,并说收敛区间只有一点x=0;如果幂级数
只在x=0处收敛,这时收敛域(即收敛点全体)只有一点x=0.但为了方便起见,我们规定这时收敛半径R=0,并说收敛区间只有一点x=0;如果幂级数 对一切x都收敛,则规定收敛半径R=+∞,这时收敛区间是(-∞,+∞).
对一切x都收敛,则规定收敛半径R=+∞,这时收敛区间是(-∞,+∞).
关于幂级数的收敛半径的求法,有下面的定理。
定理7.4.3 对于幂级数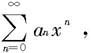 如果
如果
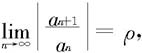
则这个幂级数的收敛半径
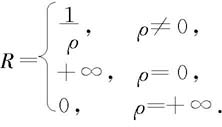
证明 考察幂级数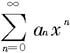 的各项绝对值所成的级数
的各项绝对值所成的级数
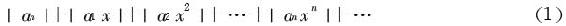
这级数相邻两项之比为
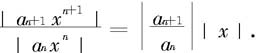
(i)如果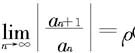 (ρ≠0)存在,根据比值判别法,则当ρ|x|<1即
(ρ≠0)存在,根据比值判别法,则当ρ|x|<1即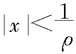 时,级数(1)收敛,从而级数
时,级数(1)收敛,从而级数 绝对收敛;当ρ|x|>1即
绝对收敛;当ρ|x|>1即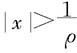 时,级数(1)发散,并且从某一个n开始
时,级数(1)发散,并且从某一个n开始
|an+1xn+1|>|anxn|,
因为一般项|anxn|不能趋于零,所以anxn也不能趋于零,从而级数 发散。于是收敛半径
发散。于是收敛半径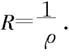
(ii)如果ρ=0,则对任何x≠0有 →0(n→∞),所以级数(1)收敛,从而级数
→0(n→∞),所以级数(1)收敛,从而级数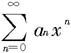 绝对收敛。于是收敛半径R=+∞.
绝对收敛。于是收敛半径R=+∞.
(iii)如果ρ=+∞,则对于除x=0外的其他一切x值,级数 必发散。于是
必发散。于是
定理7.4.4 对于幂级数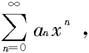 如果
如果
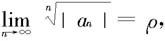
则这个幂级数的收敛半径
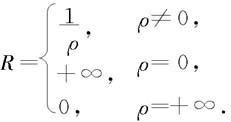
证法与定理7.4.3类似,这里略去。
例7.4.5 求幂级数
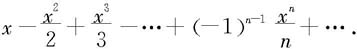
的收敛半径与收敛区间。
解 因为
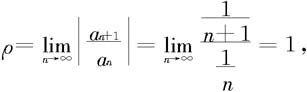
所以收敛半径
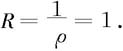
对于端点x=1,级数成为交错级数
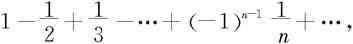
级数收敛。
对于端点x=-1,级数成为
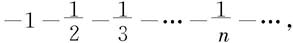
级数发散。因此,收敛区间是
例7.4.6 求幂级数

的收敛区间。
解 因为
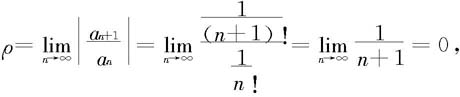
所以收敛半径R=+∞,从而收敛区间是
例7.4.7 求幂级数 的收敛半径(记号0!=1).
的收敛半径(记号0!=1).
解 因为

所以收敛半径R=0,即级数仅在x=0处收敛。 ◇
例7.4.8 求幂级数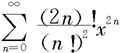 的收敛半径。
的收敛半径。
解 级数缺少奇次幂的项,定理7.4.3不能直接应用。我们根据比值判别法来求收敛半径:

当4|x|2 时级数收敛;当4|x|2>1即
时级数收敛;当4|x|2>1即 时级数发散。所以收敛半径
时级数发散。所以收敛半径
例7.4.9 求幂级数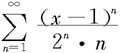 的收敛区间。
的收敛区间。
解 令t=x-1,上述级数变为
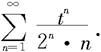
因为
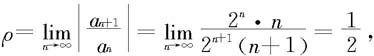
所以收敛半径R=2.
当t=2时,级数成为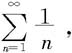 这级数发散;当t=-2时,级数成为
这级数发散;当t=-2时,级数成为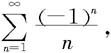 这级数收敛。因此收敛区间为-2≤t<2,即-2≤x-1<2或-1≤x<3,所以原幂级数的收敛区间为
这级数收敛。因此收敛区间为-2≤t<2,即-2≤x-1<2或-1≤x<3,所以原幂级数的收敛区间为
幂级数的性质及运算
假设幂级数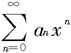 的收敛区间为I,则定义I上的函数S:
的收敛区间为I,则定义I上的函数S:

并称S为该幂级数的和函数。幂级数的和函数有许多重要性质。
定理7.4.10 设幂级数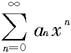 的收敛区间为I,则它的和函数S(x)在I上连续。
的收敛区间为I,则它的和函数S(x)在I上连续。
证明 对于任一点x0∈I,我们分两种情形证明S(x)在x0连续。
(i)若x0是I的内点,则存在I的内点a,b,a<b,使x0∈[a,b]⊂I.令r=max{|a|,|b|},由定理7.4.1知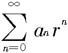 绝对收敛。于是对任何ε>0,总存在自然数N1,当n>N1时,都有
绝对收敛。于是对任何ε>0,总存在自然数N1,当n>N1时,都有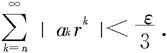
从而对任意x∈[a,b]有
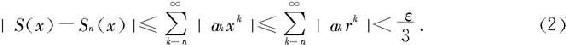
当然也有
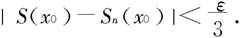
取n0>N1,由于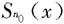 在I上连续,故存在δ>0,当|x-x0|<δ时,有
在I上连续,故存在δ>0,当|x-x0|<δ时,有
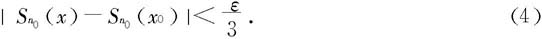
于是
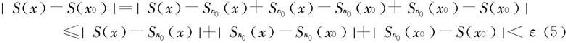
故S(x)在x0连续。
(ii)若x0是I的边界点,不妨设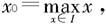 则x0>0.由于
则x0>0.由于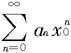 收敛,故对任何ε>0,总存在任何自然数N2,当n>N2时,都有
收敛,故对任何ε>0,总存在任何自然数N2,当n>N2时,都有
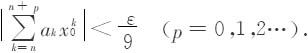
又对每个固定的x∈[0,x0], 是单调减数列,于是由阿贝尔引理有
是单调减数列,于是由阿贝尔引理有
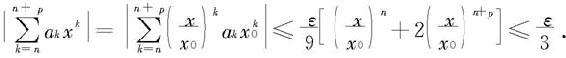
在上式中令p→∞,我们有

特别有

取定n0>N2之后,可知:存在δ>0,当x0-x<δ时,有
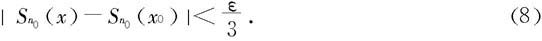
于是由(6),(7),(8)知(5)成立,即S(x)在x0连续。 □
定理7.4.11 设幂级数 的收敛区间为I,则它的和函数S在I的任何有限闭子区间[a,b]上都可积,且有
的收敛区间为I,则它的和函数S在I的任何有限闭子区间[a,b]上都可积,且有
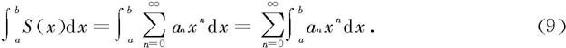
特别地,当a=0,b=x∈I时,有
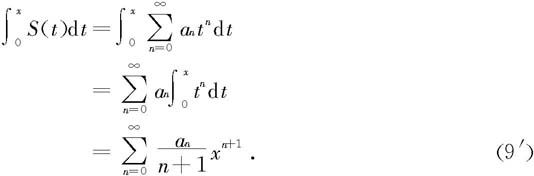
证明 由定理7.4.10知和函数S在I上连续,所以它在I的任何有限闭子区间[a,b]上可积。所以 都存在。类似于定理7.4.10的证明知,对任何ε>0,总存在自然数N,当n>N时,对一切x∈[a,b]有
都存在。类似于定理7.4.10的证明知,对任何ε>0,总存在自然数N,当n>N时,对一切x∈[a,b]有
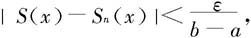
于是
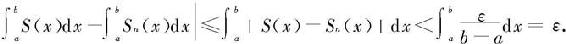
从而由极限定义有
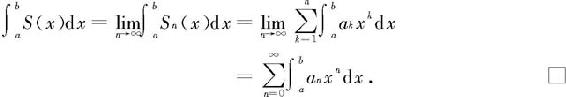
定理7.4.12 设幂级数 的收敛半径R>0,和函数为S(x),则在(-R,R)内幂级数可以逐项求导数,即对(-R,R)内任一点x,有
的收敛半径R>0,和函数为S(x),则在(-R,R)内幂级数可以逐项求导数,即对(-R,R)内任一点x,有

证明 首先,我们证明逐项求导后所得幂级数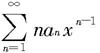 在(-R,R)中收敛。任取x∈(-R,R),则存在a,b∈(-R,R),a<b,使得x∈(a,b).令r=max{|a|,|b|},则
在(-R,R)中收敛。任取x∈(-R,R),则存在a,b∈(-R,R),a<b,使得x∈(a,b).令r=max{|a|,|b|},则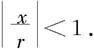 由于
由于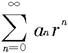 绝对收敛,故数列{anrn}有界,即存在M>0,使对一切自然数n,有|anrn-1|≤M.于是由
绝对收敛,故数列{anrn}有界,即存在M>0,使对一切自然数n,有|anrn-1|≤M.于是由
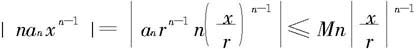
及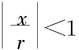 知,
知,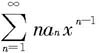 绝对收敛,因而收敛。
绝对收敛,因而收敛。
其次,我们证明(10)成立。设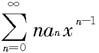 在(-R,R)中的和函数是φ(x),由定理7.4.11知
在(-R,R)中的和函数是φ(x),由定理7.4.11知

在上式两边求导得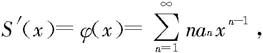 即(10)成立。 □
即(10)成立。 □
例7.4.13 利用逐项求导或逐项积分求下列级数的和函数:
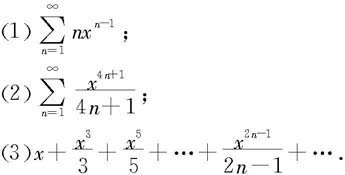
解 (1)当|x|<1时,级数 收敛。令
收敛。令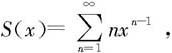 则
则
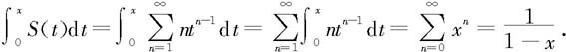
两边求导得到

(2)因为
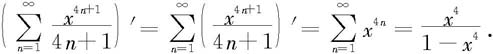
所以
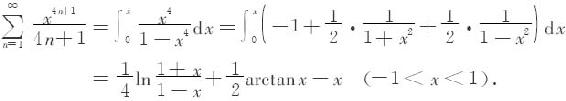
(3)因为

而
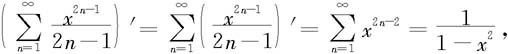
所以
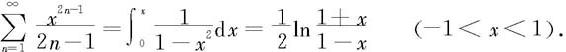
下一篇:法系的划分标准





.jpg)
.jpg)
