静止流体中的压强计算

    6.1.6　流体静压强及其特性

    1.流体静压强的定义

    在静止流体中，围绕某点取一微小面积ΔA，如图6.1-3所示，作用在该面积上的压力为ΔP，则当ΔA趋近于零时，平均压强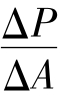的极限值即为

    该点的流体静压强，用符号p表示，即

    

    

    

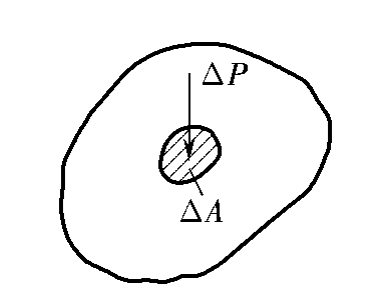
    图6.1-3

    其单位为N/m²或Pa。

    2.流体静压强的特性

    ①流体静压强垂直指向作用面，即流体静压强的方向与作用面的内法线方向相同。

    ②静止流体中任一点的静压强与作用面的方位无关。现简要证明如下。

    设在静止流体中任意方位任取一微小三棱体，如图6.1-4(a)所示，其边长分别为da、db、dc，厚度(垂直于纸面)为dl，体积为dV，作用在三个微小面积上的压强分别为p₁、p₂、p₃，则作用在三棱体上的表面力分别为

    P₁=p₁dadl，P₂=p₂dbdl，P₃=p₃dcdl

    质量力只有重力:dG=ρgdV。

    

    

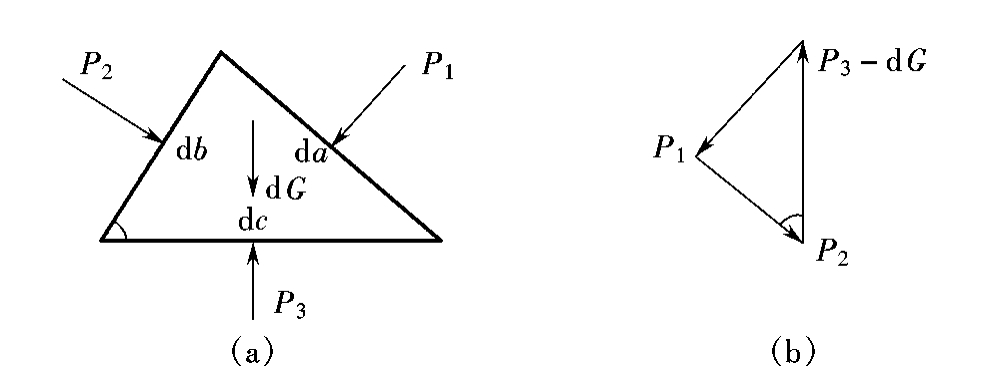
    图6.1-4

    因三棱体在P₁、P₂、P₃、dG作用下平衡，根据理论力学，必然组成一闭合力三角形，如图6.1-4(b)所示。根据几何学，这两个三角形为相似三角形，其对应边应成比例，即

    

    当da、db、dc、dl趋近于零时，三棱体收缩至一点，相应地dV也趋近于零，于是得到

    p₁=p₂=p₃

    即静止流体中任一点的静压强大小与通过该点的作用面的方位无关。至于不同空间点的流体静压强，一般来说是各不相同的，即流体静压强是空间坐标的连续函数: