
波动方程含有x、t两个自变量,它给出了任意时刻t波线上任意位置x处的质点振动的情况.为了理解波动方程的物理意义,现以式(7.4)为例作进一步分析.
(1)当x一定时,x处质点的位移y就只是时间t的函数,这时式(7.4)表示x处质点的位移随时间的变化规律,即x处的质点的简谐振动方程.
(2)当t一定时,波线上的质点的位移y只是x的函数,这时式(7.4)表示该时刻波线上各质点离开平衡位置的位移,也就是表示在给定时刻的波形.如果以y轴为纵坐标,以x轴为横坐标,可画出y-x曲线,这是一条波形曲线,也叫波形图.
综上所述,波动方程不仅表示波线上给定点的振动情况和某一时刻的波形,它也反映了质点振动状态的传播和波形的传播.
例7.2 一平面简谐波的波动方程为y=0.05cos(10πt-4πx),x、y的单位为m,t的单位为s.求该波的振幅、波速、频率和波长.
解 波动方程
与式(7.2)比较,可得
又
例7.3 如图,一平面简谐波沿x轴正方向传播,a、b为x轴上两点,相距1m.波的传播速度为u=6m·s-1,已知b点的振动方程为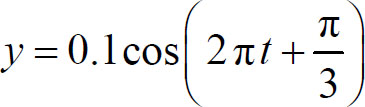
(1)以b为原点,写出波动方程;
(2)以a为原点,写出波动方程;
(3)若波沿x轴负方向传播,再以b为原点,写出波动方程.
图7.6 例7.3图
解 (1)b点的振动方程为
沿x轴正方向传播,则波动方程为
(2)由于波沿x轴正方向传播,故a点的振动超前于b点,其振动方程为
以a为原点的波动方程为
(3)若波沿x轴负方向传播,以b为原点的波动方程为
图7.7 例7.4图
解 由波形图可知,振幅A=2m,波长λ=4m,频率
圆频率
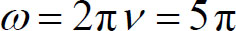
设该波传到原点时,原点处的振动方程为
因t=2s时,x=0处的位移为零,即
由波形曲线可知,该时刻原点处质点振动速度为负,所以取
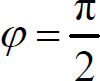
于是,原点处的振动方程为
因波沿x轴正方向传播,相应的波动方程为
上一篇:王杨卢骆当时体
下一篇:以生态安全为指向的评价指标





.jpg)
.jpg)
