光线经平行平板玻璃的折射

    5.1.2　光线经平行平板玻璃的折射

    由两个平行平面所构成的玻璃板即为平行平板玻璃。由于平面可以视为半径无限大的球面，因而平行平板玻璃也可视为焦距无限大（光焦度为零）的透镜，共轴球面系统的成像规律对其同样适用。由于平行平板玻璃被广泛用作分划板、标尺、保护玻璃、滤光镜，还由于应用广泛的反射棱镜可展开为平行平板玻璃，因此对其成像特性的研究具有重要意义。

    研究光线经平行平板玻璃的折射，就是求入射光线经互相平行的两个平面折射后，其出射光线的空间方位。如图5.2所示，与光轴交角为U₁的入射光线SA₁，与平行平板玻璃的第一面交于P₁点，入射角和折射角分别为I₁和I₁＇，折射后与第二面交于P₂点，其入射角和折射角分别为I₂和I₂＇，最终出射光线与光轴夹角为U₂＇，并与轴交于A₂＇点。由于平行平板玻璃位于空气中，因此应有：sinI₁=nsinI₁＇，nsinI₂=sinI₂＇。且由于两折射面平行，因而I₁＇= I₂，故最终有：sinI₁=sinI₂＇，即I₁=I₂＇。

    表明出射光线P₂A₂＇平行于入射光线SP₁，相应地也有U₁=U₂＇。上述结果表明，光线经平行平板玻璃折射后，其方向不改变，但将平行地移动一个距离P₂Q（=z），其对应的沿光轴位移量为A₁A₂＇=ΔL＇。

    

    

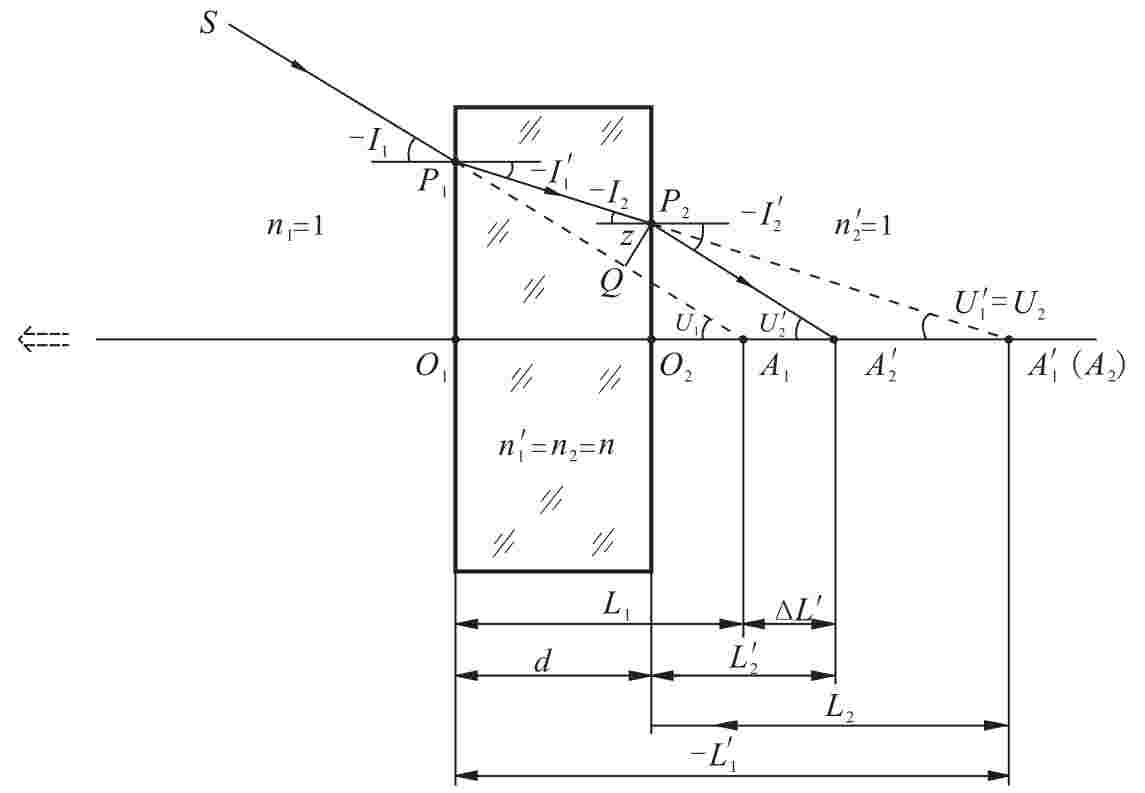
    图5.2　平行平板玻璃的折射

    由图5.2可知，侧向位移量为

    

    将上式展开可得到

    

    对应于z的轴向位移量为

    

    若以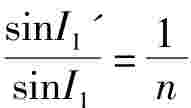代入上式，则式（5.7）又可变形为

    

    式（5.5）～式（5.8）表明，光线经平行平板玻璃折射后，其平行位移量（z，△L＇）与光线的入射角I₁（U₁）有关。由于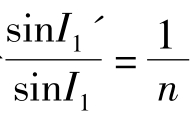，其比值为常数；因而同样角度的正切之比必非常数。因此，由A点发出的同心光束中具有不同入射角的光线，经平行平板玻璃折射后，将具有不同的轴向位移量。这说明，A点发出的同心光束，经平行平板玻璃折射后，将成为非同心光束，即成像不完善；而且，随着厚度d的增大，成像不完善的程度也将更加严重。

    不同入射角的光线所对应的像点位置由下式决定（见图5.2）：

    

    不仅不同入射角I₁所对应的像点位置不同，而且与平面折射一样，每一入射角I₁的无限细的元光束，也将发生像散。但应指出，由于物距为无限远的物点发出的是平行光束，入射角相同，折射后仍为同方向的一束平行光。因此，位于平行光路中的平行平板玻璃，不产生像差，对成像没有影响。例如，置于物镜前方的保护玻璃，对成像完全没有影响；而在物镜后方会聚光路中的平行平板玻璃（例如位于会聚光路中的反射棱镜，展开相当于平行平板玻璃）将产生像差，影响光束结构改变，因此计算光学系统时，应注意其影响。

    特殊情况在近轴条件下，入射角I₁→0，因而cosI₁≈cosI＇≈1，由式（5.7），应有近轴的轴向位移量：

    

    上式表明，Δl＇只与平行平板玻璃的厚度d和折射率n有关，而与入射角I₁无关；对给定的平板玻璃，轴向位移置Δl＇为一常量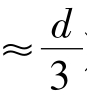（）。在平行光路中，此轴向位移量对成像没有影响；但在会聚光路中，此轴向位移量将引起像面位置移动，而且平板玻璃越厚，其位移量越大。为此，在光学系统和仪器的设计装校中必须考虑其影响，这是应该特别注意的。

    由于平行平板玻璃的平移作用，相应的近轴像点位置为

    

    平行平板玻璃符合共轴球面系统的成像规律，由（2.43）式，平行平板玻璃的近轴横向放大率应为

    

    表明，物体经平行平板玻璃成像，既不放大也不缩小。

    相应地，角放大率和轴向放大率分别为：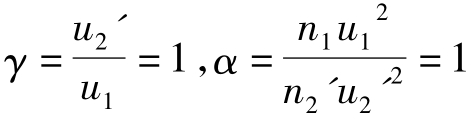

    因此，平行平板玻璃加入到光学系统的会聚光路中，只会使像面位置移动，而不会影响系统的光学特性发生变化。利用这一特性，置于物镜后方会聚光路中的摆动平板玻璃可用作光学测微器。