结晶学符号

结晶学符号_结晶矿物学

    二、结晶学符号

    （一）结晶学符号概念

    晶体被定向后，各结晶要素在空间的相对方位被确定，用简单的加不同括号的阿拉伯数字，表示晶体要素或与晶体要素有关性质在空间方位分布的特征的符号被称为结晶学符号。它包括晶面符号、晶棱（晶带轴）符号、单形符号、双晶面符号、双晶轴符号、双晶接合面符号、解理面符号等有关符号。这一章中只介绍晶面符号、晶棱（晶带轴）符号，其他符号介绍见有关章节内容。

    （二）晶面符号

    1.晶面符号概念

    晶体被定向后，晶面在空间的相对方位被确定，用简单阿拉伯数字表示晶面在空间方位分布特征的符号被称为晶面符号。

    晶面符号的表示方式有多种，一般常用的符号为米氏符号，是为纪念英国结晶学家米勒尔（W.H.Miller）而命名的。

    2.晶面符号构成

    3.三轴定向晶体晶面指数的确定

    晶体上任意晶面的指数为该晶面在三个晶轴上的截距用相应晶轴的轴单位去度量时得到的系数的倒数比来表示，晶面指数中不能出现公约数。其确定步骤如下：

    在轴单位已知条件下，晶面在三个晶轴上的截距系数为：

    OA/a₀∶OB/b₀∶OC/c₀=p∶q∶r　　　　　　（1）

    式中，OA、OB、OC分别表示晶面在X、Y、Z轴上的截距，a₀、b₀、c₀相应表示X、Y、Z轴的轴单位。p、q、r为晶面在X、Y、Z轴上的截距系数。该系数之比一定为简单的整数比（整数定律，证明省略）。

    截距系数的倒数比为：

    1/p∶1/q∶1/r=h∶k∶l　　　　　　　　　　　　　　　（2）

    h∶k∶l=a₀/OA∶b₀/OB∶c₀/OC　　　　　　（3）

    取消h、k、l间的比号，约去公因子，则得到晶面指数。

    如图4－5所示，某晶面ABC在X、Y、Z晶轴上截距依次为OA=2a₀；OB=3b₀；OC=6c₀。依据（3）可得该晶面ABC的晶面指数为：

    h∶k∶l=a₀/OA∶b₀/OB∶c₀/OC=a₀/2a₀∶b₀/ 3b₀∶c₀/6c₀=1/2∶1/3∶1/6=3∶2∶1

    所以，该晶面的晶面指数为321，该晶面符号为（321）。

    

    

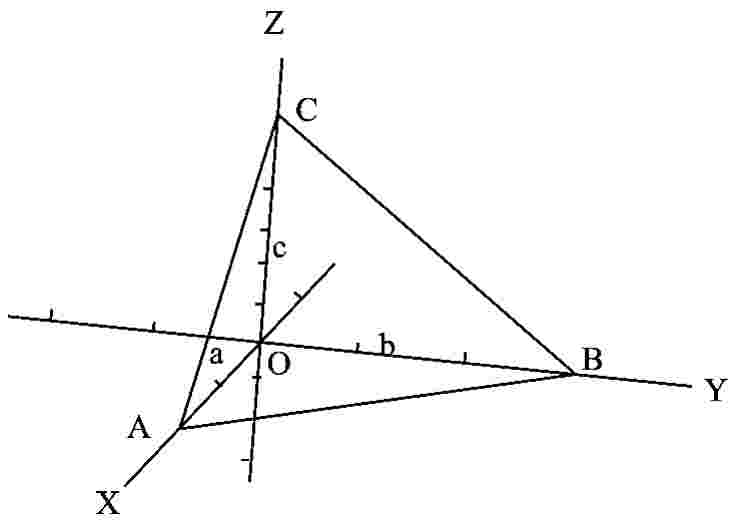
    图4－5　晶面与晶轴相交关系图

    4.四轴定向晶体晶面指数的确定

    在三、六方晶系的晶体中，为了不破坏晶体固有的对称规律，而采用四轴定向。相对应的晶面指数有四个值，即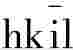（）。其确定方式与晶体三轴定向的相同，只是多一个U晶轴和一个晶面指数i而已。但对应在同一平面内的X、Y、U轴，从数学角度可知，只有两个晶轴是可独立的，另一个不独立。可得到这些晶轴相对应的晶面指数的代数和为0。即：

    

    公式（4）的数学证明见各种版本的《结晶学与矿物学》参考书籍。

    5.晶面指数含义

    （1）晶面指数中，若某一数值的符号为负，则表示晶面相交对应晶轴的负端。

    （2）如果两个晶面的晶面指数绝对值相同，而符号相反，则表示这两个晶面为平行关系。如（321）与（）为一对平行晶面。

    （3）若某一晶面的截距系数值越大，相应的晶面指数值则越小。

    （4）如某一晶面的晶面指数中，某些数值为0，则表示晶面与相应的晶轴平行。

    （5）在晶面指数中，若三个数值的绝对值相同，在高级晶族中表示该晶面与三个晶轴为等角度相交关系；在中级晶族中表示该晶面与X、Y晶轴为等角度相交关系；在低级晶族中表示该晶面与三个晶轴为不等角度相交关系。

    晶面符号在结晶学、矿物学和与之有关的科学中被广泛应用，所以要更好地学习掌握和熟练地应用。特别对由0、1、2构成的符号要熟练掌握、理解。

    （三）晶棱符号

    1.晶棱符号概念

    晶体被定向后，晶棱在空间的相对方位被确定，用简单阿拉伯数字表示晶棱在空间方位分布特征的符号被称为晶棱符号。晶棱符号也常用米氏符号形式表示。

    2.晶棱符号构成

    晶棱的米氏符号是由阿拉伯数字加中括号构成，如［110］，括号中的阿拉伯数字被称为晶棱指数。晶棱指数也按X、Y、Z轴顺序依次排列，一般记作［rst］斜体。晶棱指数可全部为正，也可部分为正，部分为负，也可全部为负。数值为正者，表示晶棱垂足相交在相应晶轴的正端；数值为负者，表示晶棱垂足相交在相应晶轴的负端，用在数值上面加“－”表示，如。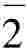

    3.三轴定向晶体晶棱指数的确定

    晶体定向后，任意晶棱的指数为将该晶棱平移到晶体中心上，选某一点作三个晶轴垂足，从垂足到坐标中心的距离为晶棱在相应晶轴的截距，用相应晶轴的轴单位去度量时得到的系数比来表示。同样，晶棱指数中不能出现公约数。其确定步骤如下：

    在轴单位已知条件下，晶棱垂足在三个晶轴上的截距系数为：

    OA/a₀∶OB/b₀∶OC/c₀=r∶s∶t　　　　　　　（5）

    式中，OA、OB、OC分别表示晶棱垂足在X、Y、Z轴上的截距，a₀、b₀、c₀相应表示X、Y、Z轴的轴单位。r、s、t为晶棱垂足在X、Y、Z轴上的截距系数。该系数之比一定为简单的整数比（整数定律，证明省略）。

    取消r、s、t间的比号，约去公因子，则得到晶棱指数。

    如图4－6所示，某晶棱OMP在X、Y、Z晶轴上垂足截距依次为OA=a₀、OB=2b₀、OC= 3c₀，依据（5）式可得该晶棱OMP的晶棱指数为：r∶s∶t=OA/a₀∶OB/b₀∶OC/c₀=a₀/a₀∶2b₀/b₀∶3c₀/c₀=1∶2∶3

    所以，晶棱OMP的指数为123，该晶棱符号为［123］。

    4.晶棱指数含义

    （1）晶棱指数中，若某一数值的符号为负，则表示晶棱垂足对应晶轴的负端。

    （2）如果两个晶棱的晶棱指数绝对值相同，而符号相反，则表示这两个晶棱为同一条晶棱，即一条晶棱可用两种符号表示。如［321］与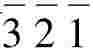［］表示同一条晶棱。

    （3）若某一晶棱垂足的截距系数值越大，相应的晶棱指数值则越大。

    

    

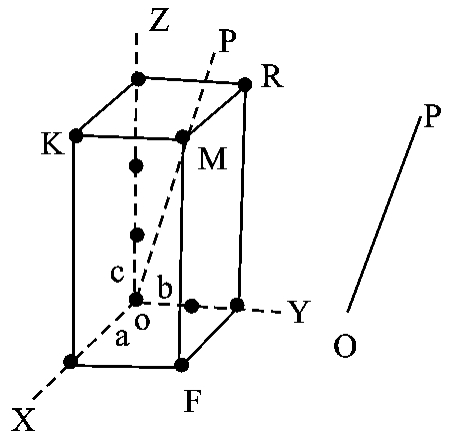
    图4－6　晶棱与晶轴相交关系图

    （4）如某一晶棱的晶棱指数中，某些数值为0，在中高级晶族及斜方晶系、单斜晶系的X、Z轴方向上表示晶棱与相应的晶轴垂直，其他晶系或其它方向上晶棱与相应的晶轴不垂直。

    （5）在晶棱指数中，若三个数值的绝对值相同，在高级晶族中表示该晶棱垂足与三个晶轴为等距离关系；在中级晶族中表示该晶棱垂足与X、Y晶轴为等距离关系；在低级晶族中表示该晶棱垂足与三个晶轴为不等距离关系。

    （四）晶带轴和晶带定律

    1.晶带概念

    一个晶带中可包含无数个交棱相互平行的晶面，既包括可以直接通过平行交棱相接触的晶面，也可以包括被其他晶带的晶面隔开但棱仍平行的晶面。

    2.晶带轴概念和符号

    每一个晶带中，都有无数个相互平行的晶棱，将这些晶棱平移到晶体中心，即坐标轴的原点上会重合成一条晶棱，而这个晶棱被称为晶带轴，它代表了一组交棱平行的晶面组合。由于晶带轴实际上是一条晶棱，所以可用该晶棱的符号作为晶带轴符号。即用［rst］表示晶带轴符号，其确定方法与确定晶棱符号的完全相同。

    如立方体中六个晶面可组成三个晶带：

    3.晶带定律

    晶体是一个封闭的几何图形，所以每一个晶面必须要与其他晶面相交，相交后至少形成两个不平行的晶棱，而这两个晶棱既属于该晶面，又分别属于另外两个晶面。而这两条不平行的晶棱则构成晶体的两个晶带。所以晶体上，任何一个晶面至少同时属于两个晶带，这一规律被称为晶带定律。如上述立方体的（100）晶面既属于［001］晶带，又属于［010］晶带。

    对这一定律也可理解为，在晶体的几何体中，任意不平行的两个晶棱（晶带轴）相交必是晶体上的一个实际的或可能的晶面；而任意不平行的两个晶面相交必是晶体上的一个实际的或可能的晶棱（晶带轴）。

    晶带定律明确地论述了晶面和晶棱相互依存、相互制约的关系，为研究晶体几何形态指明了方向。

    4.晶带轴（晶棱）符号与晶面符号的计算

    从晶带定律可知，晶体上晶面与晶棱（晶带）之间有一定制约关系，进而可从晶体上若干已知晶面或晶带（晶棱）推导或计算出一切可能的晶面或晶带的位置。

    例如晶面（hkl）位于晶带［rst］上或晶带［rst］位于晶面（hkl）之中，从平面方程式中可得出关系式为：　　　　　hr+ks+lt=0　　　　　（6）

    从公式（6）结合晶带定律可以进行以下的运算：

    ①已知两个不平行的相交晶面，求所决定的晶带（晶棱）。

    已知一个晶面的符号为（hkl），另一个晶面的符号为（mnp）求相交晶带［rst］=？

    从公式（6）得出：hr+ks+lt=0，mr+ns+pt=0

    解上两个方程得出：r∶s∶t=（kp－nl）∶（lm－ph）∶（hn－mk）

    将等式右边用二阶行列式表示为：

    

    此式特别容易记忆，即将每一晶面指数依次写两次，将两晶面的指数排成两行，用竖线隔开删去左右边两纵行，然后交叉相乘并依次取其乘积之差，依次得到想要求的指数值。

    如求晶面（110）与晶面（210）所相交的晶棱（晶带）［rst］？

    将其数值代入上行列（7）中，得到：

    

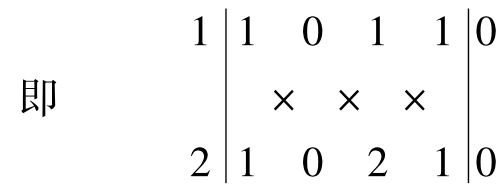
    经计算，r=0，s=0，t=－1。所求晶带为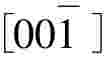，即［001］。

    ②求晶带［110］与晶带［210］所相交的晶面（hkl）？

    按照上式解法，用晶带符号取代晶面符号位置，经计算：

    h=0，k=0，l=－1。所求晶面符号为（）。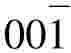

    ③已知两个晶面（dfg）与（wuy）属于同一晶带，求属于这一晶带的这两个晶面之间的晶面（hkl）？

    从晶带定律和公式（6）可知：dr+fs+gt=0，wr+us+yt=0　　　　　　　　（8）

    　　　　　　　　　　　即（d+w）r+（f+u）s+（g+y）t=0　　　　　　　（9）

    即，所求晶面的指数值为，h=（d+w），k=（f+u），l=（g+y）　　　　　（10）

    如晶面（100）与晶面（001）属于同一晶带，求同属于这一晶带的这两个晶面之间的晶面（hkl）？

    将两晶面指数数值代入公式（10）中，得到：

    h=（1+0），k=（0+0），l=（0+1），即所求晶面的晶面符号为（101）。

    ④已知两个晶带［dfg］与［wuy］包含同一晶面，求包含这一晶面的这两个晶带之间的晶带［rst］？

    计算方法同③。

    根据两个不平行晶面可以决定一个晶带，两个晶带可以决定一个晶面。利用晶体上几个有限的已知晶面可以推导出晶体上所有出现的晶面和晶棱，这对于研究晶体形貌和成因具有较大的意义。