惯性矩和惯性积

    5.4.2　惯性矩和惯性积

    

    

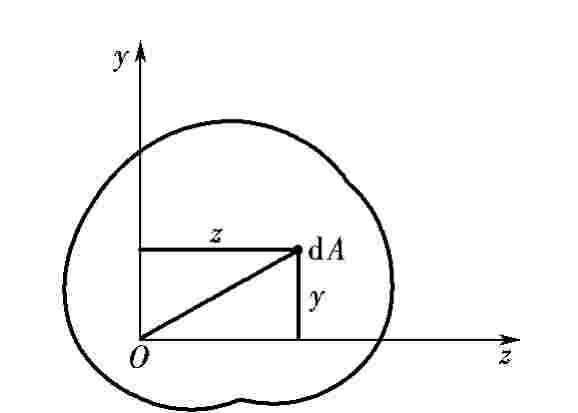
    图5.4-3

    1.定义

    设任意形状截面图形的面积为A(图5.4-3)，则图形

    

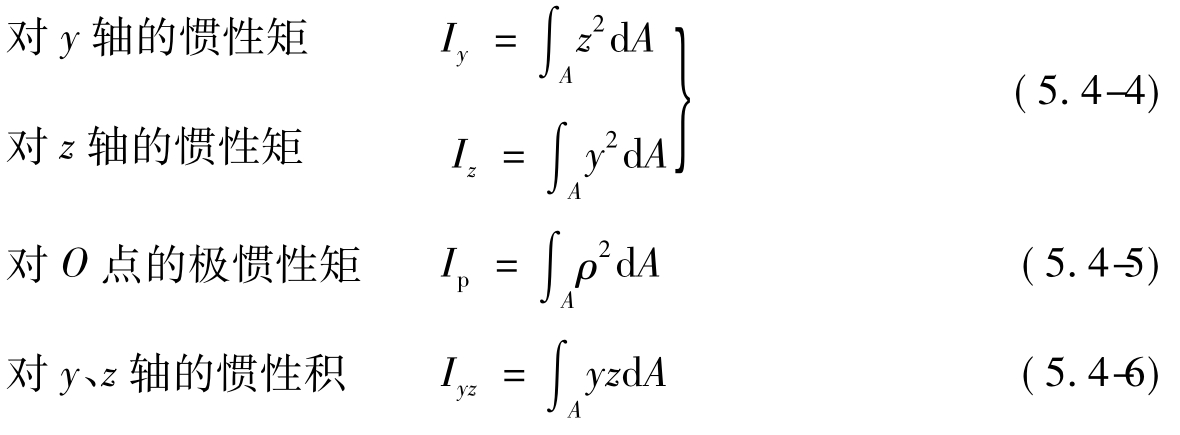
    2.特征

    ①图形的极惯性矩是对某一极点定义的，轴惯性矩是对某一坐标轴定义的，惯性积是对某一对坐标轴定义的。

    ②极惯性矩、轴惯性矩、惯性积的量纲为［L⁴］，单位为m⁴。

    ③极惯性矩、轴惯性矩其数值均为正;惯性积的数值可正可负，也可能为零。若一对坐标轴中有一轴为图形的对称轴，则图形对这一对坐标轴的惯性积必等于零;但图形对某一对坐标轴的惯性积为零，则这对坐标轴中不一定有图形的对称轴。

    ④极惯性矩的值恒等于以该点为原点的任一对坐标轴的轴惯性矩之和，即

    

    ⑤组合图形对某一点的极惯性矩或对某一轴的轴惯性矩，分别等于各组分图形对同一点的极惯性矩或对同一轴的轴惯性矩之和，即

    

    组合图形对某一对坐标轴的惯性积，等于各组分图形对同一对坐标轴的惯性积之和，即