样本估计总体的方法

参数估计_社会调查与统计

    第三节　参数估计

    一、参数估计的基本概念

    在介绍参数估计前，我们必须明确以下几个基本概念:

    总体(Population):所谓总体，简单地讲就是研究对象的全体，指具有共同性质的个体所组成的集团。对社会学的研究对象来说，更多的是指与社会、人际关系中有关事实、信息、感情、行为趋向、理由等操作化之后的数量指标。如表9-7所示，我们所调查的某个高校所有的教职员工的平均工资可以称为总体。

    样本(Sample):从总体中按一定的方式抽取的一部分称作样本，样本是由从总体中抽取的若干个个体组成的。例如，我们随机从总体中抽取的100个教职工的平均工资就是样本。样本中所包含的个体数目叫做样本容量，一般以n表示。样本有大小之分。大样本与小样本没有严格的数量界限，通常把容量小于30的样本称为小样本。样本越大，它对于总体的代表性越大，样本过小时，个别数值的变化对整体统计结果会产生较大的影响。

    统计量(Statistic):从总体中抽取容量为n的样本进行调查，可以得到一组原始调查数据，这一组原始的调查数据可以称为n个观察值或样本数据。对这样一组样本数据进行运算，可以得到样本的各项指标，比如，样本的平均数、标准差、百分比，等等，这样通过对样本中的各个个体计算而得到的样本特征量就叫统计量，它是一个相对应的随机变量产生的一个确定值。如表9-7中，我们从某高校所抽查出来的100名教职工的平均工资就是一个统计量。

    参数(Parameter):统计量描述了样本的某一特征，对于总体而言，也必定存在着相应的特征，比如，从某高校中抽取100名教职工，计算出他们的平均工资为1780元，这是样本平均数，是统计量，描述的是样本状况，对于全体教职工，也存在一个平均工资，描述总体的状况，即参数。因此，参数就是对总体的全部观测值通过计算而得到的某个特征量。社会调查的一个重要任务就是利用样本去推断预测总体，其实质就是利用样本的统计量去估计总体参数，并对这些参数给出有关检验。

    参数估计:在我们对总体进行随机抽样后，我们可以通过对样本的一些变量计算，得到许多关于样本的统计量，如样本均值、样本方差等，但是这些样本均值、样本方差就可以代表总体均值、总体方差吗?显然是不一定的。例如，当我们对总体进行重复抽样(多次抽样)时，每次抽样所得到各个样本平均数不一定相等，也不一定与总体平均数一致，但是我们可以相信一点:我们得到的样本平均数总是围绕总体平均数上下波动的。我们根据样本提供的信息对总体的某些特征(就是参数)进行估计或推断，就是参数估计。

    二、参数的点估计与区间估计

    参数的点估计即用某一数值作为参数的近似值，如利用:

    样本均值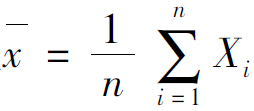直接作为总体均值μ的估计值；

    用样本比例直接作为总体比例p的估计值；

    假定我们要估计一个班学生的平均身高，根据一个抽出的随机样本计算的平均身高为166厘米，我们就用166厘米作为全班学生平均身高的一个估计值，这就是点估计。比如，我们估计一个大型公司的男女比例，根据抽样的结果为男性占60%，将60%直接作为这个公司的性别比例的估计值。这也是一个点估计的例子。

    点估计有使用方便、直观等优点，但并没有提供关于估计精度的任何信息。比如，估计的把握程度以及误差是多少，等等。为此，统计学上提出了区间估计法。区间估计就是在样本点估计的基础上，以一定可靠程度推断总体参数(θ)所在的区间范围。对于服从正态总体或者近似正态总体的参数作区间估计，其参数所在区间都可以写成如下公式(9-38):

    

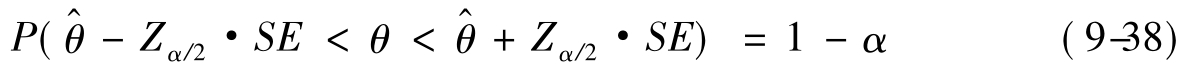
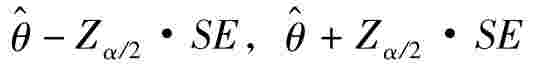    分别称为置信下限和置信上限，通称为置信限。

    α为显著性水平，1－α则称为置信度或可信度。

    从上面公式可以看出，θ^为参数的点估计，所以对参数作区间估计的关键在于标准误差SE，知道标准误差，我们可以按照上述格式，立即按置信度写出参数的区间估计的公式。

    

    表9-8　1－α，α与Z_α/2对应关系表

    

    一般地，在一定的置信度前提下，总体参数(θ)所在的范围称为置信区间或者可信区间。置信区间反映了估计的精确性，区间范围越小说明估计越是精确，在样本容量一定的情况下，置信度越高，即可靠性越大，但是置信区间越宽，表示精度越低；反之，置信度越低，即可靠性越小，但置信区间却越窄，表示精度越高。使区间估计既可靠又精确的有效方法是增加样本容量。

    1.总体平均数μ的区间估计

    因此我们把公式(9-38)的标准误差SE规定为: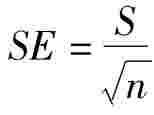，所以总体均值μ的区间估计:

    

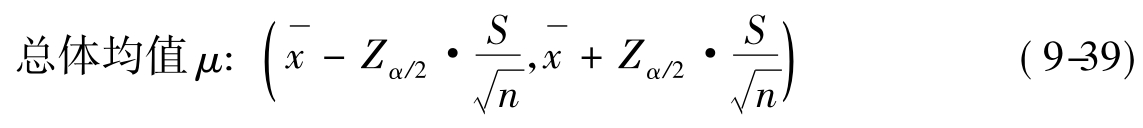
    其中: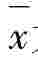为样本均值，S为样本标准差，n为样本容量。

    例14　某大学从该校学生中随机抽取100人，调查到他们平均每天参加体育锻炼的时间为26分钟，样本方差为36。试以95%的置信水平估计该大学全体学生平均每天参加体育锻炼的时间。

    解:已知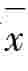=26，S=6，n=100，1－α=0.95，Z_α/2=1.96

    

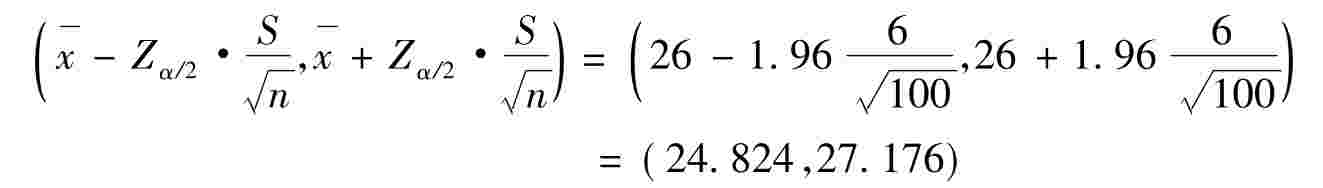
    结论:我们可以95%的概率保证学生平均每天参加锻炼的时间在24.824～27.176分钟之间，犯错的概率为5%。

    同样地，如果我要以99%的置信水平估计该大学全体学生平均每天参加体育锻炼的时间。

    则:1－α=0.99，Z_α/2=2.58

    

    可见在样本量一定的情况下，置信水平越高，可靠性越大，但相应的置信区间却越宽，估计越不精确。如果我们想使区间估计既可靠又精确，有效的方法则是增加样本容量，即增大上述公式的样本量n。

    2.总体比例的区间估计

    在社会学的研究中，有许多结果数据只能以比例或百分比表示。对于比例或百分比，同样存在区间估计的问题。我们把公式(9-38)的标准误差SE规定为: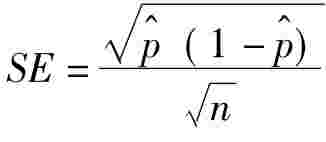，那么总体比例的区间估计为:

    

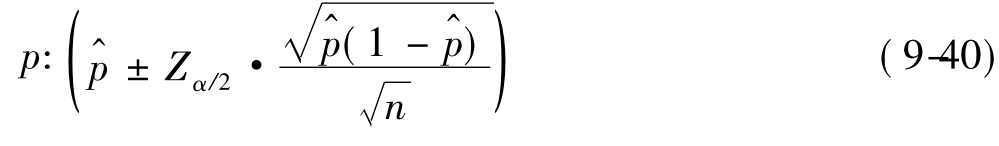
    其中: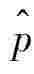为样本比例，n为样本量。

    例15　某企业在一项关于职工流失原因的研究中，从该企业职工的流失职工总体中随机选取了200人组成一个样本。在对其进行访问时，有140人说他们离开该企业是由于同管理人员不能融洽相处。试对由于这种原因而离开该企业的人员的真正比例构造95%的置信区间。

    已知n=200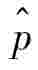，=0.7，α=0.95，Z_α/2=1.96

    

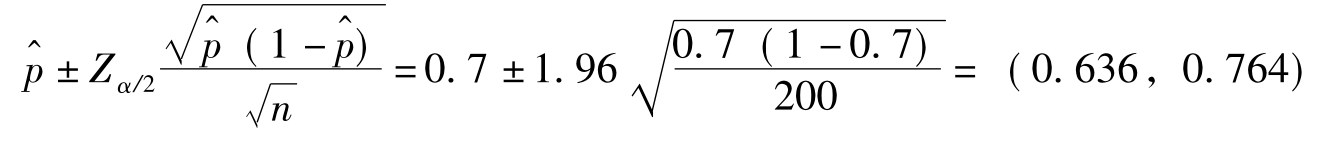
    结论:我们可以95%的概率保证该企业职工由于同管理人员不能融洽相处而离开的比例在63.6%～76.4%之间。

    3.相关系数的区间估计

    用样本相关系数r对总体相关系数ρ作区间估计，同样我们需要知道相关系数r的标准误差。计算标准误差的数学过程比较复杂，在这里我们只介绍社会统计上常用的计算方法。

    费舍(Fisher)提出了一个统计量Z，以及z与r的转换(Fisher-z转换)，其分为三个步骤:

    第一步:根据下面的公式，将样本相关系数r转换成相对应的z_r。

    

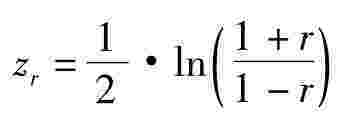
    或者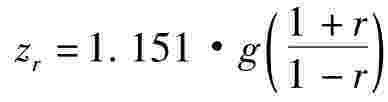　　　　　　　

    也可以通过查表求得。

    第二步:Z^的抽样分布中的标准误差，我们把公式(9-38)的标准误差SE规定为:

    

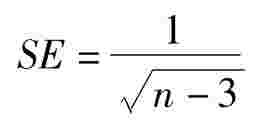
    其中:n为样本容量。

    在置信度为1－α，z_ρ的区间估计为:

    第三步:通过查表，我们可以求得z_ρ的相对应的ρ，即可得到总体相关系数ρ的区间估计。或者可以利用下面的计算公式(9-41):

    

    例16　某中级学校有1万名学生，我们随机抽取120名学生的成绩，发现其数学和语文成绩的相关系数为r=0.24，问在可信度为1－α=95%的水平，总体的数学和语文成绩的相关系数大致在什么范围内?

    已知r=0.24，则

    

    

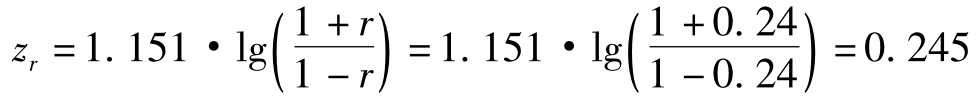
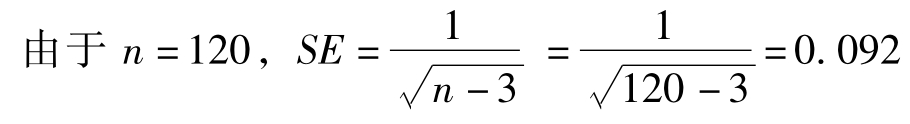
    所以我们可以写出z_ρ的区间估计:

    

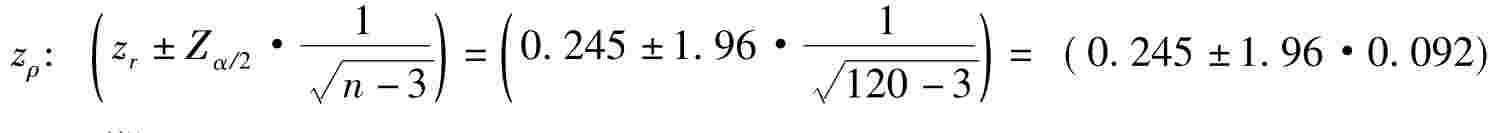
    即0.245－1.96·0.092＜z_ρ＜0.245+1.96·0.092

    0.065＜z_ρ＜0.425

    通过查表，或者利用换算公式将z_ρ换算成总体相关系数ρ可得:

    0.065＜ρ＜0.4

    总结:通过对上面内容的学习，我们可以发现，参数的估计区间的大小与置信水平和样本量是紧密相关的。如果我们对置信水平要求越高，则估计的区间就越大，它们之间呈正相关关系；若我们的样本量越多，则估计的区间就越小，估计就越精确，它们呈负相关关系。

    上面介绍了在社会统计过程中比较常用的集中参数的估计，这几种参数估计方法一般适合大样本量(n≥100)的参数估计。针对小样本量的参数估计，则需要查阅更加详细的资料。

    参数估计一般也可以在SPSS统计软件中操作完成。总体平均数的参数估计，可以通过在SPSS统计软件中的分析(Analyze)菜单下的比较均值(Compare Means)中的子菜单中的单样本T检验(One-Samples T Test)中完成。^[10]对于总体比例的参数估计的操作，作者尚未在SPSS统计软件中找到，不过在S-PLUS统计软件中的工具条上选择Statistics→Compare Samples→Counts and Proportions→Binomial Test。在这个菜单中可以完成对总体比例的参数估计。相关系数的估计，可在SPSS统计软件中的分析(Analyze)菜单下的相关(Correlate)中的双变量相关分析(Bivariate Correlations)子菜单完成。注意，这些工具都只给出它们的检验结果，而未给出它们的置信区间。