深度信念网络

    

    5.3.1　受限玻尔兹曼机

    DBN由Hinton于2006年提出[2],一个DBN模型可以看作是若干RBM堆叠构成的,因此这里先介绍RBM。

    如图5.2所示,RBM的模型图由可视层v和隐藏层h组成,同一层的单元之间没有连接,它可被认为是一个特征提取器,W为两层之间的权重。假设所有的可见单元和隐单元为二值变量,即∀i、j、v i∈0,1{},h j∈0,1{}。

    

图5.2　RBM的图模型表示

    如果一个RBM有n个可见单元和m个隐单元,用向量v和h分别表示可见单元和隐单元的状态,那么,对于一组给定的状态(v,h),RBM系统所具备的能量定义为

    

    上式中,是RBM的参数,它们均为实数。其中,W ij表示可见单元i与隐单元j之间的连接权重,a i表示可见单元i的偏置,b j表示隐单元i的偏置。当参数确定时,基于该能量函数,我们可以得到(v,h)的联合概率分布,

    

    其中Zθ()为归一化因子。

    

    由于RBM层内无连接,各隐单元的激活状态之间条件独立。此时,第j个隐单元的激活概率为

    

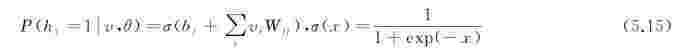
    其中,σ(x)为Sigmoid激活函数。

    当给定隐单元的状态时,各可见单元的激活状态之间也是条件独立的,即第i个隐单元的激活概率为

    

    学习RBM的任务是求出参数的值,以拟合给定的训练数据。参数θ可以通过最大化RBM在训练集上的对数似然函数学习得到,即

    

    

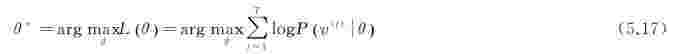
    5.3.2　深度信念网络结构

    DBN是一种生成模型,由多层RBM堆叠而成,其结构如图5.3所示。其训练过程分为预训练和全局微调两个阶段。在预训练阶段,从低层开始,每个RBM以最小化网络能量为目标单独训练,训练完后,将低层RBM抽取的特征作为高层RBM的输入训练,以此类推,通过逐层训练,直至将所有RBM训练完成。这一过程没有用到数据标签,属于无监督学习。在全局微调阶段,将之前训练阶段的网络作为DBN的初始网络,输入数据,并以数据的标签作为监督信号来计算网络误差,再通过反向传播算法对网络进行微调。

    

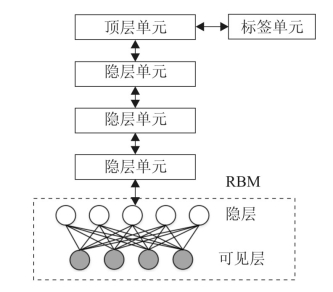
图5.3　DBN结构示意图