重新认识马尔萨斯人口论

重新认识马尔萨斯人口论_人文生态学

    第二节　重新认识马尔萨斯人口论

    英国经济学者马尔萨斯在1800年预测到：人类的人口数字将按几何级数增加，而粮食只能按算术级数增加；因此，人口的增加直到每人分给极少的食物为止。尽管马尔萨斯的理论曾经受到一些攻击，但是一个群体所得到的食物，必然受到地力的限制；事实证明这一基本情况是正确的。此外，对于某一群体，如果无限提供食物，令其自由繁殖，则其个体数字按几何级数增加，也不用怀疑。今天联合国人口基金会与很多数学家研究更实际的模型，都认为马尔萨斯的理论值得考虑。

    本节为了从人文生态学的角度来讨论人口问题，我们回忆马尔萨斯的数学模型，作为一个基础。假设人口y随时间t按比例与y而增长，则有

    

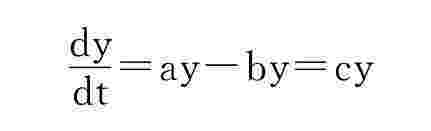
    式中的a表示增长的比例常数，因为如果在某一时间的人口基数y较大，则增长的数字亦大。由于疾病种种原因，人口还要死亡，也与y有关故又有比例常数b。令a－b＝c，利用简单的积分公式，就能看出

    y＝Ae^ct

    式中的A是一个常数，表示在t＝0时的人口数字。当c等于负数时，表示b＞a，人口在减少。

    现在我们再来看食物x的供应情况，假设食物的供应率不是无限的而是一个相当大的恒量g，则

    

    再假设维持人口每个成员生命所必需的最小平均供应率为f，则

    

    于是在食物g的供应下可以维持的最大人口数字为

    y大＝g／f

    把y大＝g／f代入y＝e^ct，得到g／Af＝e^ct；两边取对数，我们有时间

    t＝（Ln（g／fA））／c

    它表示人口y达到最大值y大所经历的时间。

    人类的人口在膨胀，根据实际调查的情况，人口的死亡数字约与y²成正比；因此，上面的马尔萨斯方程变成为

    

    式中的i与j都是生态常数。利用积分公式，则得到

    

    这里的K是积分常数。当t＝0时，由此式看出人口达到最大值。这表示y大只与常数i和j有关，而不像原来的马尔萨斯方程中的y大与食物供应率g及f相关。

    如果i／j＝g／f，则人口增长的情况就返回到马尔萨斯的理论；这当然是一个非常偶然的情况。一般说来，人口会把自己增加到趋近最大值的情况；这时的人口依赖于食物的最大供应量g，因此，g／f＞i／j