
傅里叶级数的系数决定于周期函数的波形。通过观察周期函数波形的某种对称性,可预见哪些系数存在,哪些系数为零,同时还能简化求这些系数的运算。下面讨论3种常见的周期函数的对称性。
(1)周期函数f(t)是奇函数,即f(t)=-f(-t),函数的波形对称于坐标原点,如图5-3所示,则傅里叶级数中只含有正弦项,不含恒定分量和余弦项,即
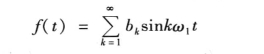
(2)周期函数f(t)是偶函数,即f(t) =f(-t),函数的波形对称于纵轴,如图5-4所示,则傅里叶级数中只含有恒定分量和余弦项,而没有正弦项,即
![]()
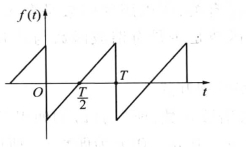
图5-3 周期性奇函数
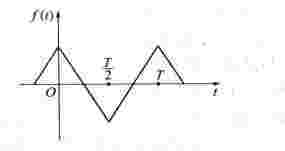
图5-4 周期性偶函数
(3)若周期函数f(t)前后半波对称,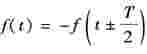 ,如图5-5所示,则傅里叶级数中只含有奇次谐波,即
,如图5-5所示,则傅里叶级数中只含有奇次谐波,即
所以f(t)称为奇谐波函数。
证明
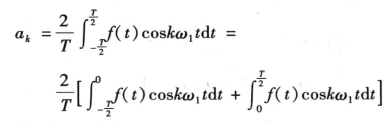
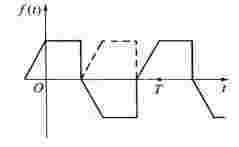
图5-5 前后半波对称的函数
把上式等号右端第一个积分式中的t以![]() 代替,则得
代替,则得
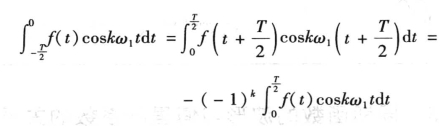
所以
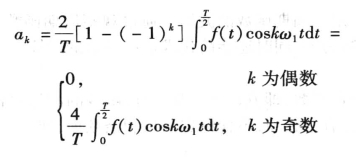
同理可得
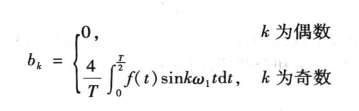
证毕。
应当指出:由于系数ak和bk与计时起点的选择有关,所以周期函数是奇函数或偶函数,不仅与函数波形有关,还与计时起点选择有关。但函数是否是奇谐波函数与计时起点选择无关,只与函数波形有关。
例5-1 图5-6所示为矩形波,求其傅里叶级数展开式。
解 图5-6所示的矩形波既是偶函数,又是奇谐波函数,所以f(t)的傅里叶展开式中既不含正弦项,又不含恒定分量和偶次谐波,即bk=0,a0=0,ak =0(k为偶数)。所以
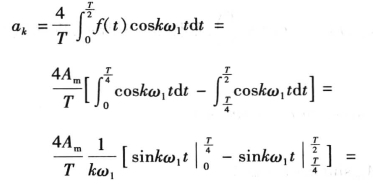
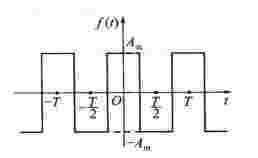
图5-6 例5-1图
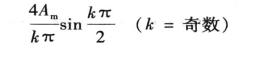
所以
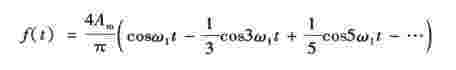
下一篇:档案整理方法





.jpg)
.jpg)
