一阶电路的阶跃响应

    

    在分析动态电路过渡过程时，利用单位阶跃函数描述电路的激励和响应是比较方便的。下面先介绍单位阶跃函数，然后再介绍单位阶跃响应。

    1.单位阶跃函数

    单位阶跃函数的数学定义是：

    单位阶跃函数ε（t）的波形如图6-27（a）所示。它在t=0点处不连续，有一台阶形跃变，跃变幅度为1。

    将单位阶跃函数ε（t）乘以K，则得一般的阶跃函数f（t） = Kε（t），如图6-27（b）所示。它在t=0点处跃变幅度为K，即

    

    延迟单位阶跃函数和延迟阶跃函数分别为

    

    

图6-27　单位阶跃函数和阶跃函数

    和

    

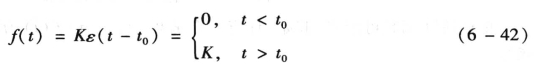
    它们的波形如图6-28（a）、 （b）所示。

图6-28　延迟单位阶跃函数、延迟阶跃函数

    阶跃函数可用来描述开关的动作。图6-29（a）用来表示在t=0时把电路接到1V直流电压源上；图6-29（b）用来表示在t = t0时把电路接到2A的直流电流源上。

    阶跃函数可用来表示矩形脉冲。图6-30（a）所示的矩形脉冲可看作两个阶跃函数组成的，如图6-30（b）所示。

    

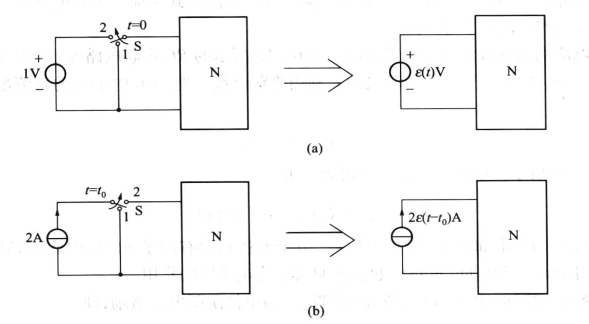
图6-29　用阶跃函数表示开关动作

图6-30　用阶跃函数表示矩形脉冲

    单位阶跃函数可用来“起始”任意一个函数f（t）。设f （t）为所有t都有定义的任意一个函数，则

    

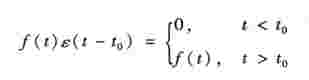
    其波形如图6-31所示。

    

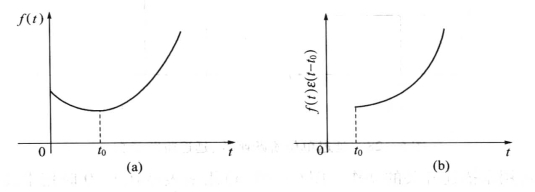
图6-31　单位阶跃函数的“起始”作用

    2.一阶电路的阶跃响应

    动态电路对（单位）阶跃激励的零态响应称为（单位）阶跃响应。如果电路是一阶的，其响应就是一阶电路（单位）阶跃响应。

    阶跃响应的求解方法与6.4节相同。图6-13所示的RC串联电路处于零原始状态，t=0时闭合开关，电路与直流电压源Us接通。利用阶跃函数可把t=0时加入的直流电压源Us表示为

    

    如图6-32（a）所示。电路的零态响应可表示为

    

    其中τ=RC， uC的波形如图6-32（c）所示。由于表达式含有因子ε（t），因此不必说明这些表达式只适用于t ≥0的区间，ε（t）已起到说明表达式定义域的作用。

    如令图6-32（a）中Us =1V，则输入（激励）为单位阶跃电压激励，即

    

    

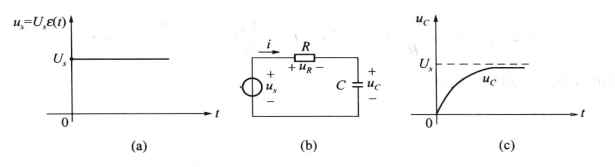
图6-32　阶跃响应

    则电路的零态响应为单位阶跃响应，即

    

    式中：s（t）单位为V，波形如图6-33（a）所示。

    对于t = t0时加入的单位阶跃电压激励，即

    根据电路的时不变性质，其单位阶跃响应也延迟了时间t0，即

    

    波形如图6-33（b）所示。

    

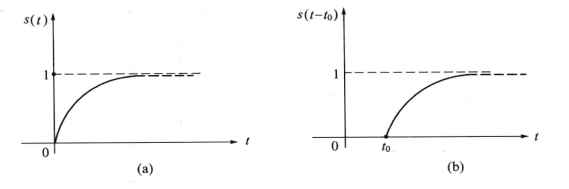
图6-33　单位阶跃响应

    例6-13　图6-34（a）所示的矩形脉冲电压在t=0时作用于RL串联电路，求其零态响应i。

    解　（1）把矩形脉冲电压分解为两个阶跃电压，如图6-34（c）所示，即

    （2）分别求两个阶跃电压作用下的零态响应

    

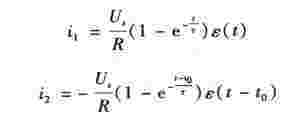
    （3）电路的零态响应为两个阶跃响应的叠加

    

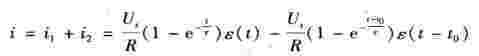
    响应的波形如图6-34（d）所示。

    

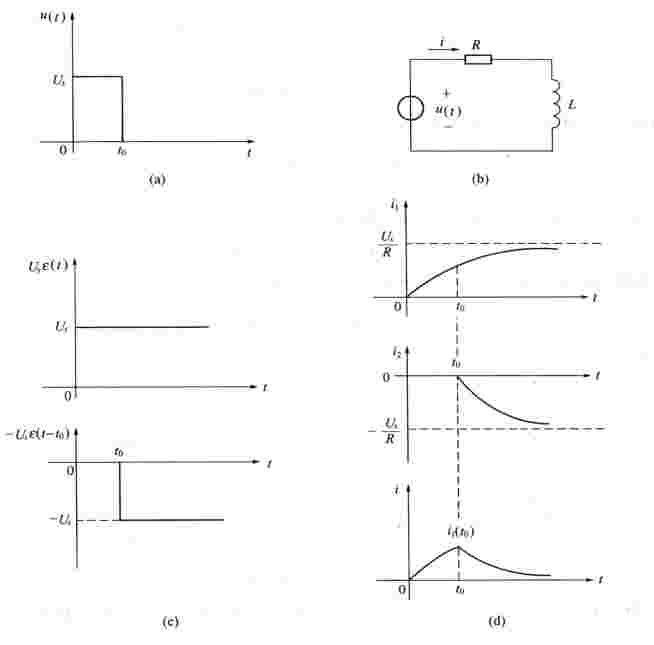
图6-34　例6-13图