股利现金流量折现模型

    

    股票的预期价格是由未来股息所决定的,因此,股票的价值就是无期限的股息折现后的价值:

    

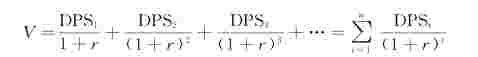
    式中,V为每股股票的价值;DPS t为第t期的预计支付的每股股利;r为股票的要求收益率。

    如果能够准确地预测股票未来每期的股利,就可以利用公式计算股票的内在价值了。在对股票未来每期股利进行预测时,关键在于预测每期股利的增长率,用g t表示第t期股利的增长率,其数学表达式为:

    

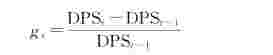
    根据对股利增长率的不同假设,股利现金流量折现模型可以分为零增长模型、匀速增长模型(戈登模型)、两阶段增长模型等。

    (一)零增长模型

    零增长模型是股利贴现模型的一种特殊形式,也是最简单的一种形式。它假设每期的股利都是一样的,股利的增长率为零。即:

    DPS1=DPS2=DPS3=…=DPS n

    或者 g t=0

    可以得到:

    

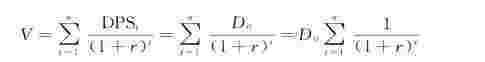
    简化后,得

    【例2-1】 A公司是一家零增长型公司,该公司每年发放的股利为5元/每股,投资者要求的最低报酬率为10%,则A公司目前股票的内在价值为50元。计算过程如下:

    

    如果在二级市场上,A公司的股价为49元/股,则说明该公司股票可能被低估,投资者应该在二级市场上购入该公司股票。

    (二)匀速增长模型(戈登模型)

    匀速增长模型又称戈登(Gordon)模型,是股利贴现模型的另一种特殊形式。它假设每期支付的股利增长额都以稳定的增长率g增长。

    匀速增长模型的运用有三个前提假设条件:

    (1)股息的支付在时间上是永久性的。(t→∞)

    (2)股息的增长速度是一个常数。(g t=g)

    (3)模型中的贴现率大于股息增长率。(r﹥g)

    根据上述三个前提假设条件,可以将公式改写为:

    

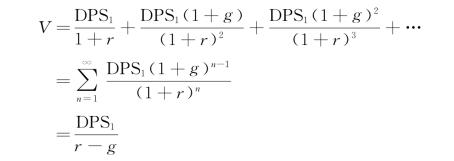
    式中,DPS0,DPS1分别表示初期和第一期支付的股利。

    当式中的股息增长率g等于零时,匀速增长模型就变成了零增长模型。所以,零增长模型是匀速增长模型的一种特殊形式。

    【例2-2】 A公司刚刚支付了每股2元的股利,投资者要求的最低报酬率为10%,投资者预计每年的股利将按照5%的增长率稳定增长,则下一年的股利为2×(1+5%)=2.1元。按照上述公式计算,A公司的股票内在价值为:

    

    如果该股票在二级市场上的价值为45元/股,则说明该公司股票可能被高估,投资者应该考虑在二级市场上出售该公司股票。

    (三)两阶段增长模型

    匀速增长模型是建立在假设公司各期红利都按固定比例增长的基础上的。但事实上,很少有公司能做到这一点,从而衍生出两阶段增长模型等非匀速增长模型。

    两阶段增长模型是将公司的发展分成两个阶段,在这两个阶段中,股息的增长率不同,分别用g 1、g 2表示。例如,一家公司拥有一项专利,保护期为5年,因此5年内增长率会比较高;保护期过后,增长率会下降到平均水平,因此该公司第一个阶段是高成长阶段;第二个阶段是稳定成长阶段。如图2-1所示。

    

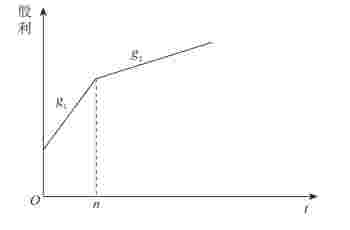
图2-1　两阶段增长模型

    当我们使用两阶段增长模型时,关键是分别计算出第一和第二阶段的股票价值,加总计算股票的内在价值。即:

    V=V 1+V 2

    式中 V——股票价值;V 1——第一阶段股票价值;V 2——第二阶段股票价值。

    在第一阶段,分别计算第1年至第n年的股利现值,加总可得第一阶段的股票价值,即:

    

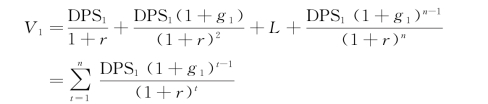
    而在计算第二阶段股票价值时,关键在于计算出第二阶段期初的股利,再利用匀速增长模型(戈登模型)加以折现,就可以得到第二阶段股票价值,即:

    

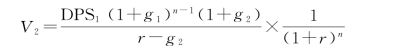
    综合上述三个公式,可以得到计算两阶段增长模型的股票内在价值的公式:

    

    与两阶段增长模型类似,三阶段增长模型等非匀速增长模型也可以采用类似的方法进行计算。

    【例2-3】 A公司最近支付了每股2元的股利,预计在以后3年内股利将以12%的年增长率增长,在接下来的3年内年增长率为8%,此后预计以5%的年增长率一直增长。假定投资者要求的报酬率为12%,那么股票的内在价值是多少?

    该股票的价值计算如下: