第二节 抽样推断原理
一、几个基本概念
（一）全及总体与样本总体
全及总体，又称总体或母体（Population），是指所要调查研究对象的全体。如要调查某一地区的人口情况，则该地区的全部居民便构成一个总体。全及总体的单位数用字母“N”表示。
样本总体，又叫子样或样本（Sample），是从全及总体中随机抽取出来，用于代表全及总体的那部分单位的集合体。样本总体的单位数称为样本量（Sample size），通常用字母“n”表示。一般来说，样本量n远小于总体单位数N。在抽样中，样本单位数达到或超过30的样本称为大样本，而单位数不足30的属于小样本。
对于某一具体问题来说，全及总体是惟一确定的，而样本总体则不是惟一确定的，因为从总体N中抽取容量为n的样本（当n＜N时）有多种抽法。
（二）放回抽样与不放回抽样
放回抽样（Sampling with replacement）即从总体N中随机抽取一个容量为n的样本，每次抽取一个样本单位，经调查记录后将该单位重新放回总体，然后抽下一个单位，这样连续进行n次即得到样本总体。放回抽样中每次抽取样本单位都是在完全相同的条件下进行的，每个单位被抽中的概率相等。
（三）总体参数与样本统计量
总体参数就是表示全及总体数量特征的指标。设总体单位数为N，总体各单位标志值为Xi（i＝1，2，…，N），有以下总体参数：
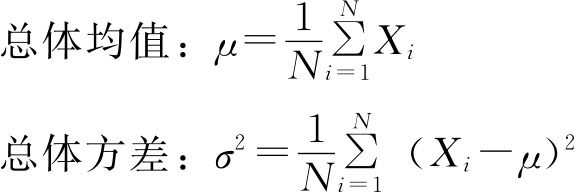
又设总体N中具有某种性质的单位数为N1，不具有这一性质的单位数为N0，则有
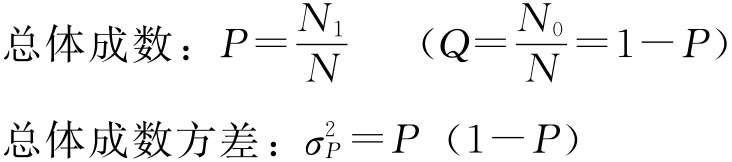
对于某一具体问题来说，总体是惟一确定的，因此总体参数也是确定的。但总体参数通常是未知的，抽样调查的目的就是通过对样本的研究来推断总体参数，以达到对总体的认识。
样本统计量就是描述样本数量特征的指标。设样本量为n，样本各单位标志值为Xi（i＝1，2，…，n），另外，在n中具有某种性质的单位数为n1，不具有这一性质的单位数为n0，则有以下样本统计量：
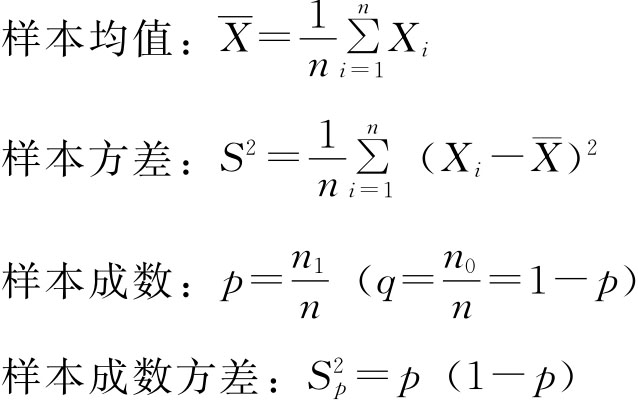
二、抽样分布
由于从某一总体N中随机抽取容量为n的样本有多种抽法，因此，样本统计量不是惟一确定的，而是随机变量，并且各种变量值出现的次数可能有多有少。由样本统计量的全部可能取值和相应的概率组成的分布数列称为样本统计量的抽样分布。
（一）样本均值的抽样分布
样本均值的抽样分布即指全部样本均值的可能取值和与之相应的概率的对应关系，若把这种对应关系用图描述出来，就是样本均值的抽样分布图，如图5－2所示。
数理统计中的有关抽样定理揭示了样本均值抽样分布的两个重要结论：
第二，如果总体变量X不服从正态分布，或不知其分布，但具有均值μ和方差σ2，那么，从该总体中随机抽取容量为n的样本，根据独立同分布的中心极限定理，当n充分大时，有
因此，在总体方差σ2已知的大样本情况下，无论总体为何分布，样本均值均服从或近似服从正态分布；对于小样本，如果总体为方差已知的正态总体，样本均值也服从正态分布。但是，不同的抽样方法，其分布的特征值略有不同。
放回抽样：
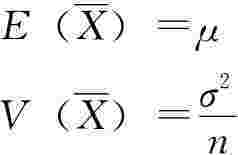
不放回抽样：
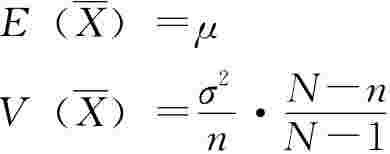
上述结论表示多数情况下样本均值的抽样分布为正态分布，其分布可用图5－2表示。
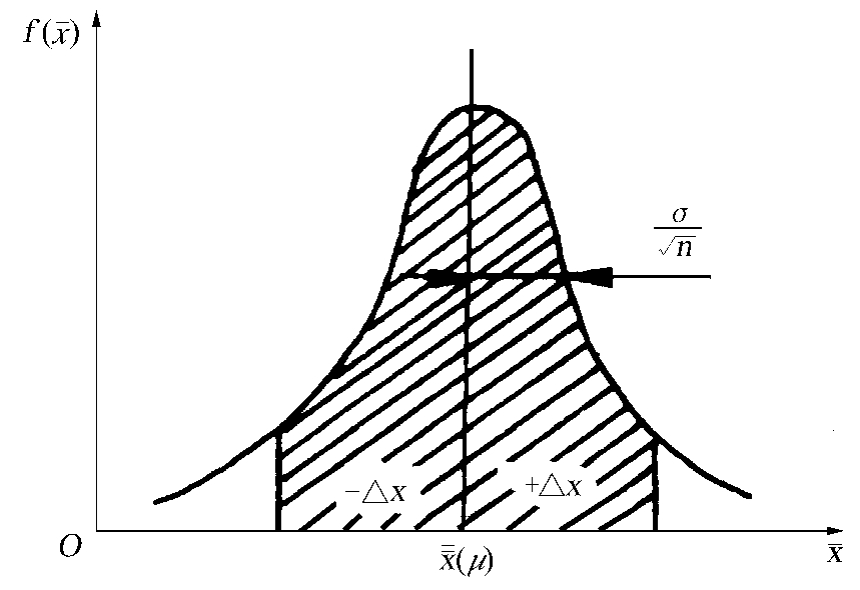
图5－2 样本均值的分布
其密度函数为
由正态分布的性质可知：
1.样本均值的均值等于总体均值，即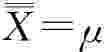
；
2.全部可能样本的样本均值与总体均值的平均离差程度就是抽样分布的标准差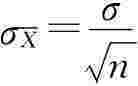
，在分布图上表示为曲线的拐点到对称轴间的距离；
3.图中阴影部分面积为样本均值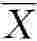
落在总体均值μ某一区间［μ－ΔX，μ＋ΔX］的概率，通过对样本均值正态分布进行标准化转换，运用标准正态分布表，可以计算出概率的具体数值。举例说明如下：
例5－1：设总体有5个单位，其标志值分别为X1＝10，X2＝20，X3＝30，X4＝40，X5＝50；总体变量X服从均值μ＝30，标准差σ＝14.14的正态分布。现从总体中随机抽取容量n＝2的样本，计算样本均值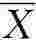
落在［25，35］内的概率。
标准化变量
所以，概率
查附录二表1标准正态分布表，当Z＝0.5时，2Φ（0.5）－1＝0.383，即样本均值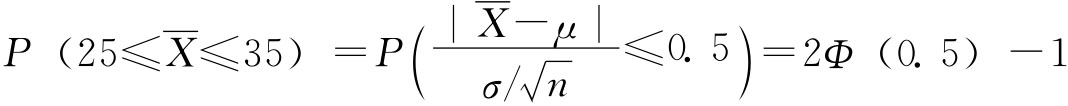落在［25，35］内的概率为38.3%。
若样本抽自方差未知的正态总体，则样本均值服从自由度为n－1的t分布，记作：
在前面随机变量函数的分布中已述，当n≥30时，t分布与正态分布相差无几，因此，总体方差未知的样本均值，大样本时近似服从正态分布，小样本时服从上述t分布。
（二）样本成数的抽样分布
成数虽属于0—1分布，但由前述重要结论的第二点可知，在放回抽样的情况下，随着样本量n的增大，样本成数趋于正态分布，即：
因此，在大样本的情况下，可以用样本均值的抽样分布原理计算样本成数落在总体成数一定区间内的概率。
如果进行的是不放回抽样，则
当样本量很小时，样本成数p不再近似服从正态分布，而是服从二项分布，即p～B（n，p）。
（三）样本方差比的抽样分布
.jpg)
