战前人口分布和影响因素

战前人口分布和影响因素_中国近代城市文化的动态发展： 人文空间的新视野

    三、战前人口分布和影响因素

    各地区地理环境不同，能容纳的人口数量将有很大的差别。以通常情形而论，大抵山地人口不如平原人口之密，游牧区人口不如农耕区之密。⁽³⁾

    影响人口分布的最主要因素就是人们的物质生产方式，尤其是生产力发展水平以及生产布局特点。但这一切在任何时候都离不开一定的自然环境的基础，无论人们的物质生产方式在将来可能进步到何种程度，这一点是不会改变的。⁽⁴⁾除此之外，人口密度还受人文社会因素（如离中心城市的距离）的影响。需要引人严谨的定量分析的方法加以验证。

    （一）相关分析

    为探究各种自然因素与人口密度是否存在相关性，运用统计学中的相关分析（Bivariate Correlation）来确定。本文使用Pearson相关系数，又称Pearson积矩相关，其计算公式为：

    

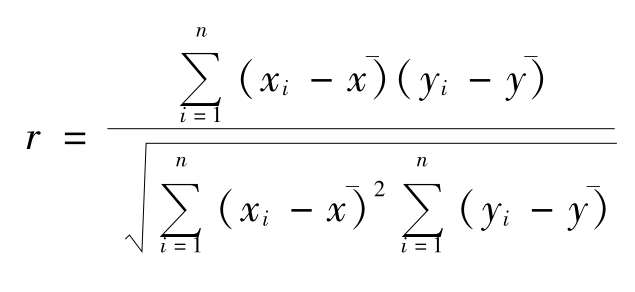
    当|r|＝1时，称为完全线性相关；当0＜|r|＜1时，存在相关。当r＞0时，称为正相关；当r＜0时，称为负相关。

    为了进行定量分析，我们首先运用ArcGIS软件对空间数据进行处理。在Spatial Analysis中的extract Value to point工具分别获得各县的海拔高度、降水、积温、温度和土地适宜类型的平均值（中国土地适宜类型：利用1∶1 000 000土地资源地图矢量化数据，抽取其中土地适宜类层，采用内插方式，计算格网点数据。分为九个类型，分别为宜农耕地类、宜农宜林宜牧土地类、宜农宜林土地类、宜农宜牧土地类、宜林宜牧土地类、宜林土地类、宜牧土地类、不宜农林牧土地类、湖泊或其他）；Spatial Analysis中的Surface Analysis中Slope、Aspect工具分别获得各县级单元的坡度和坡向；Near工具获得县级单元（以几何中心代表其位置）到水系（河流）的距离和到中心城市的距离。

    从表1中可以看出人口密度与各个自然因素之间关系统计上都具有显著性，尤其与海拔高度、坡度、温度、土地适宜类型、河流距离、中心城市距离相关性较高，显著水平为0.001。但是与坡向、降水的相关系数较低，虽然统计上仍然显著（显著水平分别为0.01和0.05）。

    

    表1　各项指标与人口密度的相关分析

    

    

    注：a显著性在0.001；b显著性在0.01；c显著性在0.05。

    （二）人口密度与地形因素

    从人口的垂直分布看，全国70%以上的人口，集中分布在面积仅占全国1/4的海拔500米以下的地区，其中200米以下的平原地带的人口约占全国的50%。海拔2 000米以上的地区，虽然也占全国总面积的1/4，但人口比重却不足1%。海拔在3 000米以上地区，城市和居民点的分布数很少。总的趋势是海拔越高人口越少，和世界多数国家近似。为了分析人口的分布与海拔、坡度是否存在一定的关系，我们借用统计分析的手段。

    考虑多个自变量的多元线性回归方程可表示为：

    y＝α＋∑_iβ_ix_i＋ε，

    式中α和β_i是回归模型的参数，被称为回归系数；ε是随机误差项或随机扰动项，反映了除x_i和y之间的线性关系之外的随机因素或不可观因素。表2列出了多元线性回归中各种地形因素对人口密度的影响。

    

    表2　地形因子多元线性回归分析

    

    

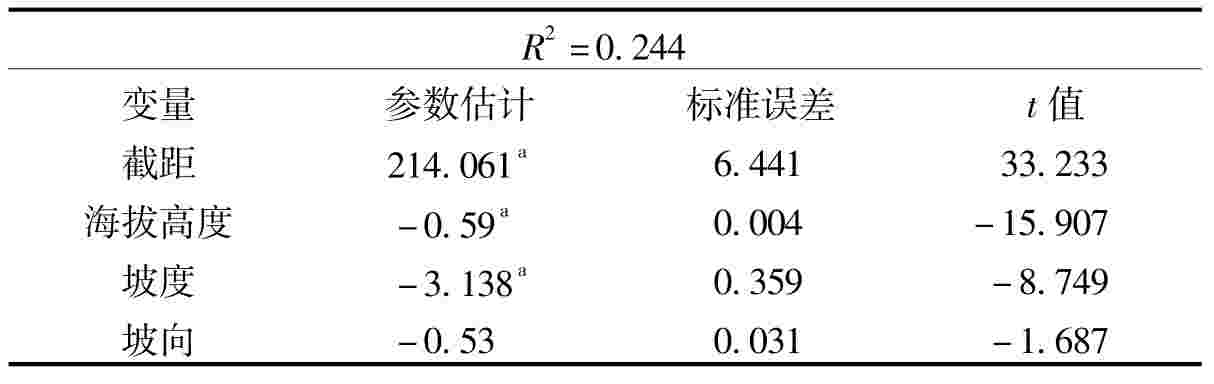
    注：a显著性在0.001。

    表2的结果显示，地形因子与人口密度在统计上十分显著。即海拔越高、坡度越大，人口密度越低。而坡向对人口密度的影响并不显著。

    （三）人口密度与水文因素

    一般来说，有河流经过的地方，水资源丰富、利于农耕，并且为交通运输提供了便利，因此对人口分布有一些影响。这里，我们用离最近河流的距离刻画水文因素对人口密度的影响。由于只有一个自变量，只需要用一元线性回归的手段。结果如表3。

    

    表3　水系距离与人口密度一元线性回归分析

    

    

    注：a显著性在0.001。

    从表3中可以看出，距离水系越近，人口密度越高，虽然回归系数不高，但在统计上还是显著的。说明水文这个自然因素的影响是可能存在的，但单靠这一个因素是不能很好地说明人口的分布情况，还要考虑其他因素。

    （四）人口密度与农业相关因素

    我国是农业大国，尤其是在1936年，农业人口在总人口中占了绝大部分。土壤、水热条件是影响农业的关键因素。

    表示热量条件分布的指标多种多样，如各种温度指标和无霜期等指标，其中积温是一个较好的综合指标。积温是指植物从播种到成熟，要求一定量的日平均温度的累积⁽⁵⁾。本文也将采用积温这个指标。从降水量来看，我国年雨量分布的主要特点是东南多、西北少，从东南向西北递减⁽⁶⁾。而年降水量400mm的分界线与中国人口分界线瑷珲—腾冲一线基本一致。土壤也是农业生产最基本的条件之一。

    我们利用前面提到的多元线性回归模型来分析人口密度与农业相关因素的关系。

    

    表4　人口密度与农业相关因素多元回归分析

    

    

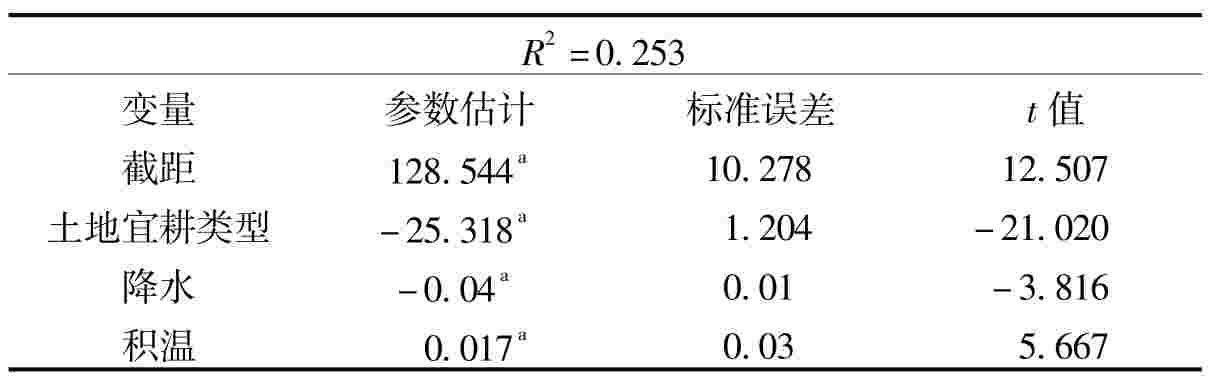
    注：a显著性在0.001。

    从表4显示的结果可以看出，土地宜耕类型、降水以及积温这些农业相关因素对人口密度的影响在统计上都十分显著。其中，降水量的影响是负值，与我们的预想相反，原因是降水量与土地宜耕类型高度相关，当土地宜耕类型对人口密度的影响大大超过降水量的影响时，掩盖了降水的真实影响。统计上称为“自变量互相关”（collinearity）。这一问题也说明了后面因子分析法的必要性。

    （五）人口密度与中心城市

    中心城市是指对较大地域范围具有强大吸引力和辐射力的综合性职能的大中城市，离中心城市越近，到市场的运输成本越低，土地利用强度越大，人口密度越高⁽⁷⁾。以沈阳为例，从图4可以清楚地看出，以沈阳为中心城市，其周边的县受其吸引力的影响，距离沈阳越近、人口密度越高的趋势。

    为了全面分析中心城市的影响，本文选取民国时期十个重要城市，分别是上海、汉口、天津、广州、南京，沈阳、青岛、重庆、北平和哈尔滨。根据GIS，距离的度量为每个县（以其几何中心代表）离其最近的中心城市的直线距离。同样，由于只有一个自变量，只需要用一元线性回归的手段。结果如表5。

    

    

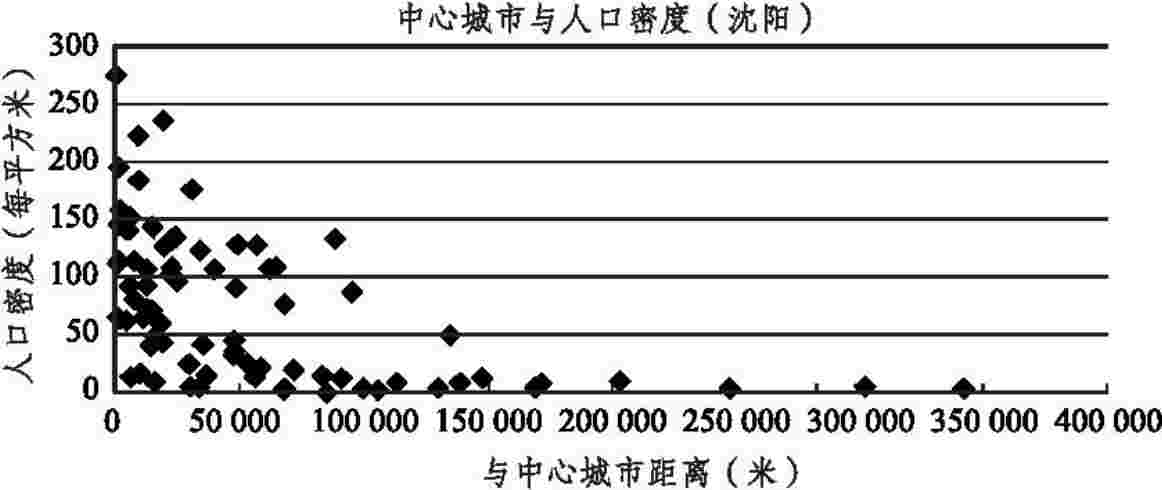
    图3　1936年中心城市与人口密度

    

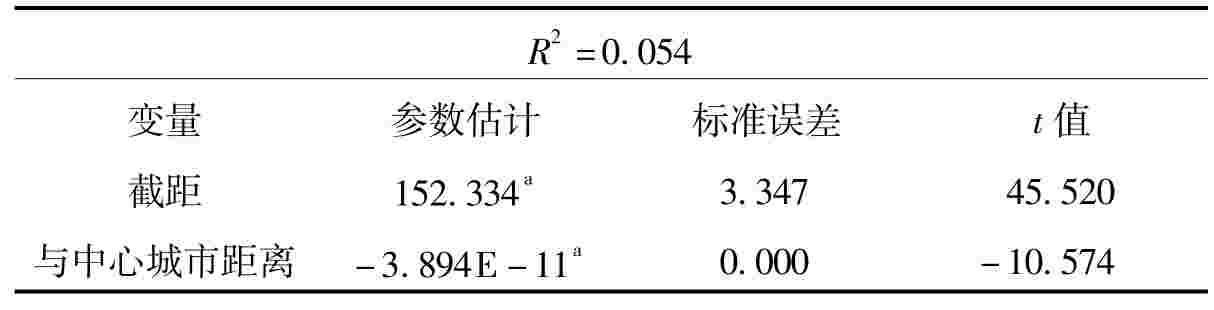
    表5　到中心城市距离与人口密度一元线性回归分析

    

    

    注：a显著性在0.001。

    从表5中可以看出，距离中心城市越近人口密度越高。虽然在统计上显著，但回归系数不高。

    （六）人口密度影响因素综合分析

    人口分布密度是受各种因素综合影响的。有些因素之间会存在如前所述的“自变量互相关”（collinearity）的问题，给分析解释回归结果带来困难。这里我们运用统计学中的因子分析方法，通过数据降维的方式，将原来可能互相关的多变量整合成较少的几个独立的综合因子。

    因子分析的一般模型如下：

    x₁＝a₁₁F₁＋a₁₂F₂＋…＋a_1mF_m＋ε₁

    x₂＝a₂₁F₁＋a₂₂F₂＋…＋a_2mF_m＋ε₂

    ……

    x_p＝a_p1F₁＋a_p2F₂＋…＋a_pmF_m＋ε_p

    其中x_i（i＝1，2，…，p）是原始变量标准化后的值，F_j（j＝1，2，…，m）表示不可观测的因子组成的向量，a_ij（i＝1，2，…，p；j＝1，2，…，m）被称为因子载荷，ε_i（i＝1，2，…，p）是相互独立的误差项。因子载荷a_ij是第i个变量与第j个因子之间的相关系数，反映了第i个变量在第j个因子上的重要性，即表示变量x_i依赖于因子F_j的比重。

    为了检验本文所涉及样本数据是否适合进行因子分析，我们首先进行了KMO（Kaiser-Meyer-Olkin）检验和巴特利特（Bartlett）球形检验。KMO统计量取值在0和1之间，其值越接近于1，意味着原有变量间的相关性越强，越适合作因子分析。本文样本数据的KMO值为0.71，根据经验，该数据比较适合做因子分析。另外，巴特利特球形检验法也是以原有变量间相关系数为基础的。它的零假设相关系数矩阵是一个单位阵（对角线的所有元素均为1，非对角线的所有元素均为0），也就是原有变量相互独立。基于我们的数据，巴特利特球形检验法的统计量是5 420.8（自由度36），显著水平超过0.001，拒绝零假设。再次表明相关系数矩阵不是单位阵，原有变量之间存在相关性，适合进行主成分分析。

    从表6中的特征值和累计方差比例两个指标中可以看出，选取3个因子，解释了总方差的2/3是比较合适的。

    

    表6　主成分分析的特征值

    

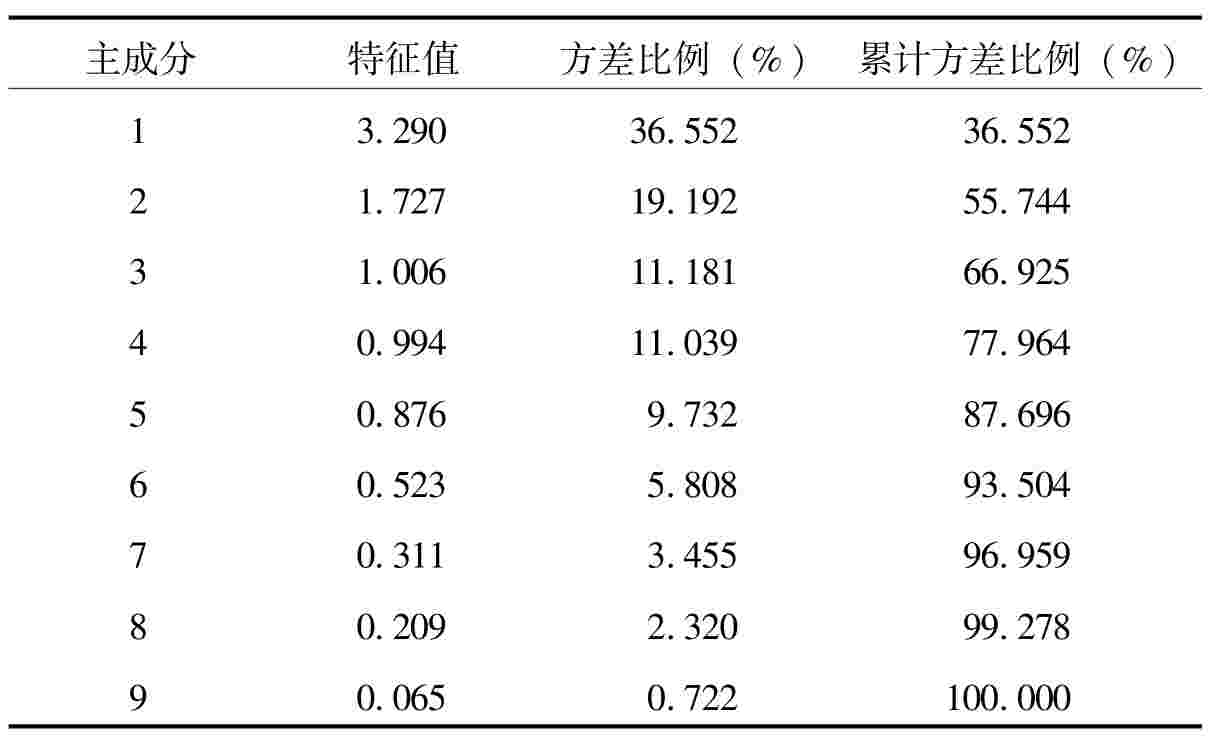
    在统计分析软件SPSS中还可以得到各主成分的负荷系数和贡献率。为了使因子特征更加突出，因子矩阵更加清晰，我们运用方差最大旋转法对因子进行旋转。表7为旋转后的主成分因子负荷矩阵。

    

    表7　旋转后主成分因子负荷矩阵

    

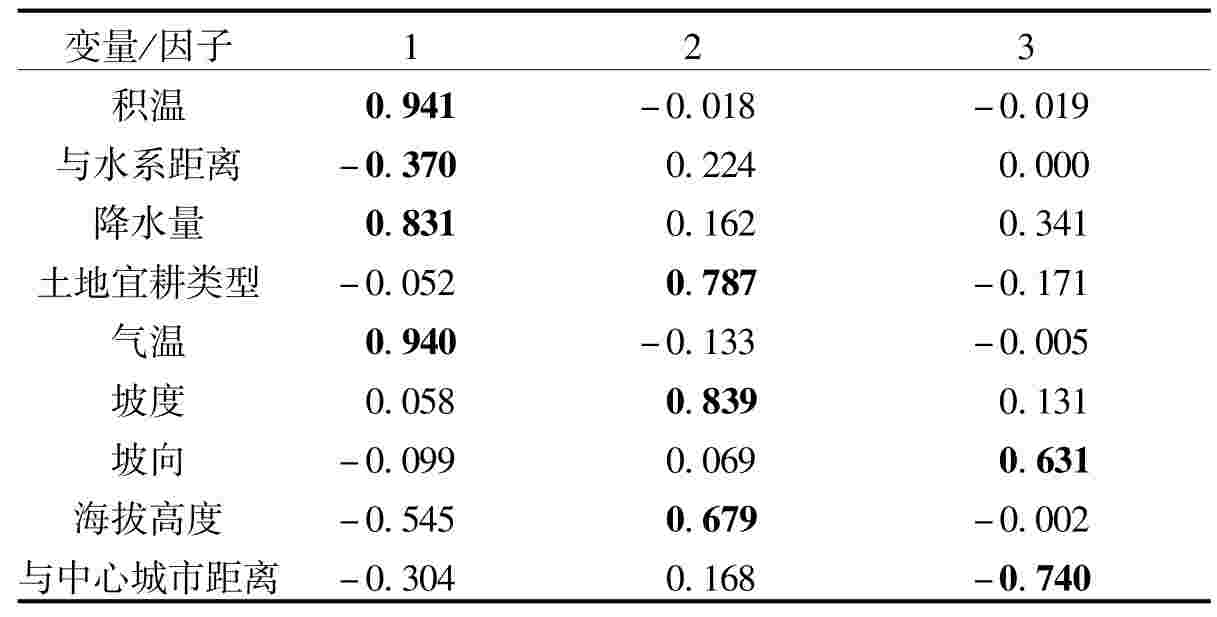
    由表7中可以看出其中第一主成分因子取代了原始数据中的积温、与水系距离、降水量还有气温值这四项变量，可以概括为气候指标。第二个主成分解释了总方差中的54.604%，包含土地易耕类型、坡度、海拔高度这三个变量，可以概括为土壤及地形指标。第三主成分，包含坡向和与中心城市距离两个变量，可以概括为与中心城市距离指标。

    为了进一步确定因子1、因子2、因子3与人口密度的确切关系，我们再次使用上文提到的线性回归方法，并且为了使回归方程更加精确，我们用人口密度的对数作为因变量。得到结果如表8所示。这一回归模型可以解释1936年中国县级人口密度空间变化的57.7%，而且三个因子统计上都很显著。

    

    表8　三个主要因子的多元回归分析

    

    

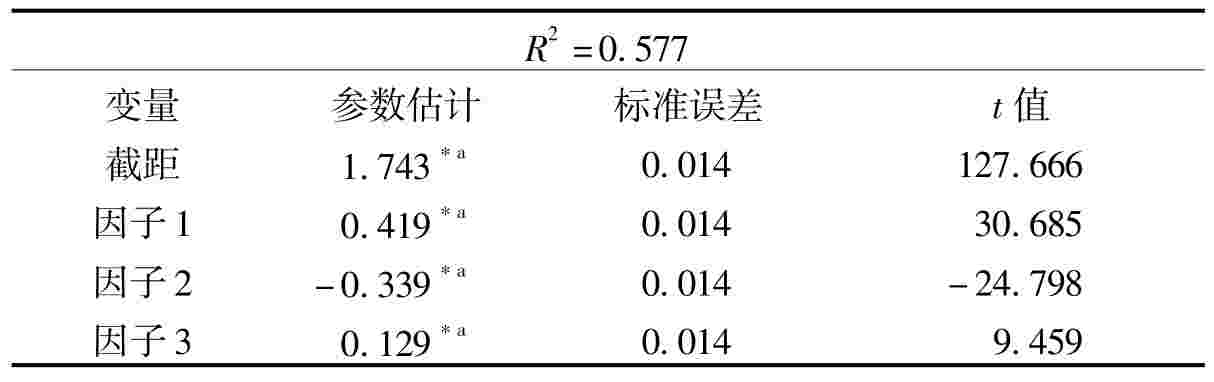
    注：*a显著性在0.001。