
由欧拉公式得
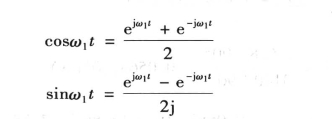
因此,周期函数的傅里叶级数展开式可改写为
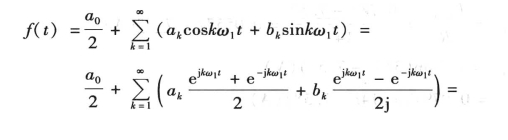
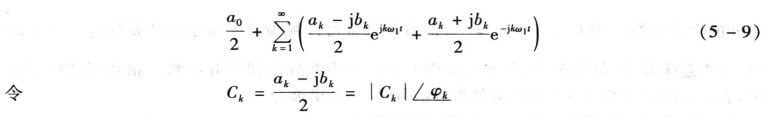
复数Ck的模与辐角分别为
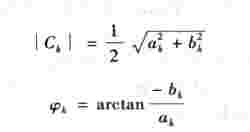
由傅里叶系数公式(5-2)知,系数ak是谐波次数k的偶函数,bk是谐波次数k的奇函数,即
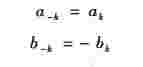
所以
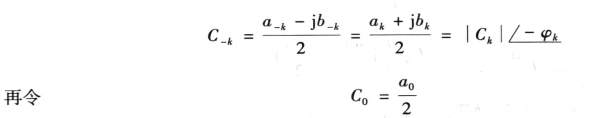
则式(5-9)可写为
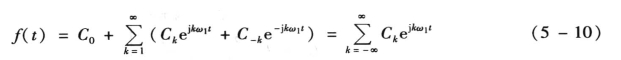
式(5-10)就是傅里叶级数的指数形式。
复系数Ck的计算公式可根据傅里叶系数ak和bk的计算公式导出,即
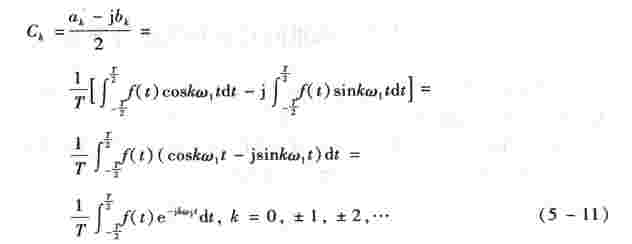
令式(5-11)中的k =0,则有
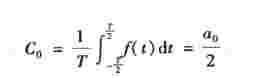
在傅里叶级数的指数形式表达式中,即式(5-10)中,谐波次数k的取值是从-∞到+∞之间的全部整数。当k =0时,![]() ,即恒定分量可以视为频率为零的谐波分量。当k <0时,是否意味着有“负频率”的谐波存在呢?否!因为在导出傅里叶级数的指数形式的过程中,表示各次谐波的三角函数化为复指数函数时,一个谐波分量是由两个同频率的共轭复指数函数合成的(见式(5-9)),而不是只取一个正频率或负频率的复指数函数来代表一个谐波分量。所以“负频率”的谐波分量是不存在的。
,即恒定分量可以视为频率为零的谐波分量。当k <0时,是否意味着有“负频率”的谐波存在呢?否!因为在导出傅里叶级数的指数形式的过程中,表示各次谐波的三角函数化为复指数函数时,一个谐波分量是由两个同频率的共轭复指数函数合成的(见式(5-9)),而不是只取一个正频率或负频率的复指数函数来代表一个谐波分量。所以“负频率”的谐波分量是不存在的。
例5-6 图5-9所示的矩形脉冲电压,其脉冲幅值为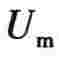 m,脉冲持续时间(脉冲宽度)为τ,脉冲重复周期为T。试将此矩形脉冲电压展开为傅里叶级数的指数形式。
m,脉冲持续时间(脉冲宽度)为τ,脉冲重复周期为T。试将此矩形脉冲电压展开为傅里叶级数的指数形式。
解 根据式(5-11)

图5-9 矩形脉冲电压
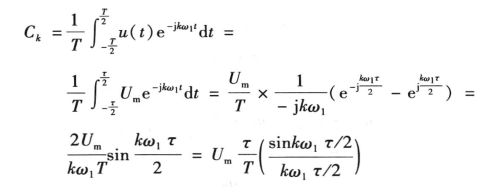
式中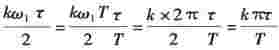 ,故上式又可写为
,故上式又可写为
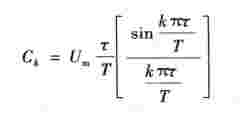
下一篇:增值税税率为0的征税范围





.jpg)
.jpg)
