物质波的衍射现象

    第四节　物质波的衍射现象

    物质波

    1923年，法国物理学家路易·德布罗意分析经典物理学中力学与光学的对应关系时，试图把爱因斯坦发现的光的波粒二象性推广到所有粒子。他认为其他实物粒子（如电子、中子、质子等）也具有波动性，并把爱因斯坦建立的光量子的有关公式应用到实物粒子上，得到实物粒子的能量和动量公式。ε＝mc²＝hν

    

    式中，ε为能量；ν为频率；p为动量；λ为波长；m为粒子质量。

    由以上公式可以得到实物粒子的波长公式为

    

    这就是著名的德布罗意波长关系式。以上三个公式被称为爱因斯坦德布罗意关系。

    于是，德布罗意提出：一切运动的实物粒子与光子一样，也有波粒二象性。把实物粒子对应的波称作德布罗意波或物质波。

    物质波的衍射现象

    1927年，美国的戴维孙和他的合作者革末从实验上证实了电子衍射现象，从而证明了德布罗意波的存在。

    

    

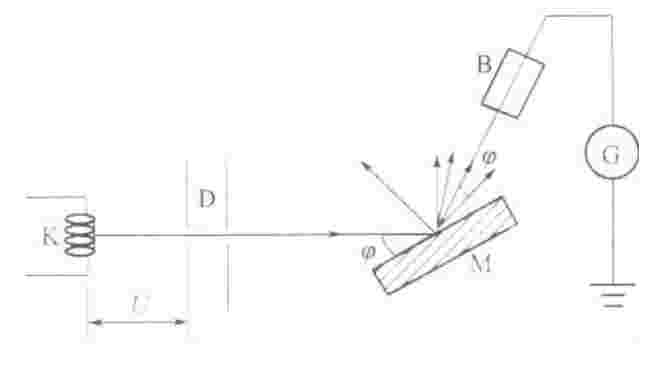
    电子在晶体上衍射实验示意图

    上图是戴维孙和革末的实验装置示意图。从加热灯丝K出来的电子经电势差U加速后，通过一组栏缝D以一定角度投射到镍单晶体M上，经晶面反射后用集电器B收集，进入集电器的电子流强度I可用与B相连的电流计G来测量。实验结果是：在某一掠射角p下，电子流强度I不是随U_KD增大而单调增大，而只有当电势差为某些特定值时，电子流才有极大值。

    理论分析方法与x射线在晶体上反射很相似，不是粒子。电子波长公式为

    

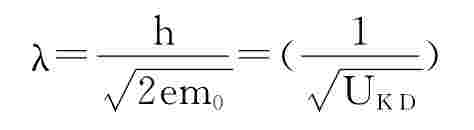
    代入x射线晶体衍射布拉格公式得

    

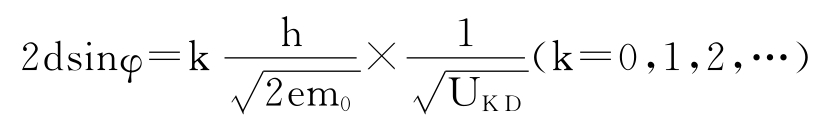
    式中，d为晶格常数；φ为掠射角，e为电子电量；h为普朗克常数；U_KD为K、D两点之间所加的电压。

    即电势差满足上式时，电子流强度为最大值。这意味着电子具有波动性。由此计算所得的电势差的各个量值和实验结果相符合，从而证明了德布罗意的假设和德布罗意波长公式的正确性。

    1927年，英国物理学家汤姆父子观察到了衍射环。根据这些圆环的半径可以计算出电子波的波长，从而令人信服地证明了德布罗意波长公式，证实了电子的波粒二象性。后来，接连发现了物质波的衍射现象，1929年，伊斯特曼和斯特恩成功地研究了原子和分子的衍射。1936年，在约里奥实验室工作的冯哈尔巴恩和普赖斯沃克获得了中子衍射的实验证据。

    几十年来，德布罗意的物质波思想成了量子理论的起点。

    由于电子具有波动性，可用电子束代替光束，设计制成电子显微镜。

    海森伯的测不准关系

    在经典力学中，物体在轨道的任一点具有确定的位置和速度，或者说物体的坐标和动量同时具有确定值。对微观粒子来说，由于具有波粒二象性，轨道概念已失去意义。那么，是否仍可用上述的经典概念和方法去描述微观粒子的运动状态呢？

    其适用程度和准确性又是如何呢？对此，1927年海森伯提出测不准关系，又叫不确定关系。

    设粒子的运动是一维的，例如，沿x轴运动，当粒子经过某处时同时测出其位置和动量的不确定量分别为△x和△p_x，则两者之间存在如下的制约关系。

    

    式中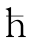＝h／2π，也叫普朗克常数。

    测不准关系是波粒二象性及其统计关系的必然结果。其意义是：不能同时准确测量微观粒子的位置和动量，即对粒子的位置测量得越准确，则对动量的测量就越不准确，反之亦然。

    海森佰不确定关系指出，粒子位置的不确定性乘上动量的不确定性不能小于一个确定量——普郎克常数。并且，这个极限既不依赖于测量粒子位置和速度的方法，也不依赖于粒子的种类。海森佰不确定性原理是微观世界的一个基本性质。

    在不确定性原理的基础上，海森佰、薛定谔和狄拉克运用这种手段将力学重新表达成称为量子力学的新理论。在此理论中，粒子不再有分别被很好定义的、能被同时观测的位置和动量，而代之以它们的结合物的量子态。

    微观粒子的其他力学量，如能量、角动量等一般也都是不确定的。如果微观粒子处于某一状态的时间为出△t，其能量必有一个不确定量△E，两者关系为

    

    称为能量和时间的测不准关系。