竖曲线设计

    纵断面上两相邻不同坡度线的交点称为变坡点。 为保证行车安全、舒适以及视距的需要，在变坡处设置的纵向曲线即为竖曲线。 相邻两坡度线的交角用坡度差“ω”表示，坡度角一般较小，可近似地用两坡段坡度的代数差表示，即ω＝i2-i1，式中i1，i2分别为两相邻坡段的坡度值，上坡为正，下坡为负。 如图4.2所示。 ω为正，变坡点在曲线下方，竖曲线开口向上，称为凹形竖曲线；ω为负，变坡点在曲线上方，竖曲线开口向下，称为凸形竖曲线。

    各级道路在变坡点处均应设置竖曲线。 竖曲线的线形采用二次抛物线。 由于在其应用范围内，圆曲线与抛物线几乎没有差别，因此，竖曲线通常表示成圆曲线的形式，用圆曲线半径R来表示竖曲线的曲率半径。

    图4.2 竖曲线示意图

    1.竖曲线的计算

    （1）用二次抛物线作为竖曲线的基本方程式

    在图4.3所示坐标系下，二次抛物线一般方程为：

    对竖曲线上任意点P，其斜率为：

    当x＝0时，i＝i1；x＝L时，i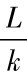＝＋i1＝i2，则：

    抛物线上任一点的曲率半径为：

    式中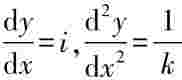，代入上式，得：

    R＝k（1＋i2）3／2

    因为i介于i1和i2之间，且i1，i2均很小，故i2可略去不计，则：

    R≈k （3）

    将（2）式和（3）式代入（1）式，得二次抛物线竖曲线基本方程为：

    式中 ω——坡差，％；

    L——竖曲线长度，m；

    R——竖曲线半径，m。

    图4.3 竖曲线要素示意图

    图4.4 竖曲线几何元素

    （2）竖曲线几何要素计算

    竖曲线的几何要素主要有竖曲线切线长T、曲线长L和外距E，如图4.4所示。

    L＝R·ω （4.4）

    （3）竖曲线上任意点纵距y的计算

    式中 y——计算点纵距；

    x——计算点桩号与竖曲线起点（或竖曲线终点）的桩号差。

    （4）竖曲线上任意点设计标高的计算

    ①计算切线高程。

    H1＝H0-（T-x）·i （4.8）

    式中 H0——变坡点标高，m；

    H1——计算点切线高程，m；

    i——纵坡度。

    其余符号如图示。 利用该式可以直接计算直坡段上任意点的设计标高。

    ②计算设计标高。

    H＝H1±y （4.9）

    式中 H——设计标高，m；

    “±”——当为凹形竖曲线时取“＋”，当为凸形竖曲线时取“-”。

    其余符号意义同前。

    2.竖曲线设计标准

    竖曲线的设计标准有竖曲线最小半径和竖曲线长度。 由于在凸形竖曲线上和在凹形竖曲线上汽车行驶时的受力及视距等考虑因素的不同，凸形竖曲线和凹形竖曲线又有不同的设计标准。

    （1）竖曲线最小半径

    1）凹形竖曲线极限最小半径

    凹形竖曲线极限最小半径主要从限制离心力、夜间行车前灯照射的影响以及在跨线桥下的视距3个方面计算分析确定。

    ①从限制离心力不致过大考虑。 汽车行驶在竖曲线上，由于离心力的作用，要产生失重（凸形竖曲线）或增重（凹形竖曲线）。 失重直接影响乘客的舒适感，增重则不仅影响乘客的舒适感，还对汽车的悬挂系统产生超载的影响。 竖曲线半径的大小直接影响离心力的大小，因此，必须首先从控制离心力不致过大来限制竖曲线的极限最小半径。

    汽车在竖曲线上产生的离心力为：

    则

    式中 F——汽车转弯时受到的离心力，N；

    F／G——单位车重受到的离心力。

    根据日本资料限制为F／G＝0.028，代入上式得：

    图4.5 夜间行车前灯照射距离

    ②从汽车夜间行驶前灯照射距离考虑。 如图4.5所示，若照射距离小于要求的视距长度，则无法保证行车安全。 按此条件即可推导出此时凹形竖曲线的最小半径的计算公式。

    设汽车前灯高度为h，向上的照射角为β，由竖曲线计算公式得：

    由图可知：

    BC＝h＋s·tanβ

    两式联解得：

    式中 s——前灯照射距离，m，按行车视距长度取值；

    h——前灯高度，m，取h＝0.75m；

    β——前灯向上的照射角，取δ＝1°。

    将s、h、β取值代入式（4.12）得：

    ③从保证跨线桥下的视距考虑。 为保证汽车穿过跨线桥时有足够的视距，也应对凹形竖曲线最小半径加以限制。

    综合分析以上3种情况后，技术标准以限制凹形竖曲线离心力条件为依据，即采用式4.10制定出凹形竖曲线极限最小半径的规定值，见表4.11和表4.12。

    表4.11 公路竖曲线最小半径和最小长度

    表4.12 城市道路竖曲线最小半径和最小长度

    2）凸形竖曲线极限最小半径

    凸形竖曲线极限最小半径主要从限制失重不致过大和保证纵面行车视距两个方面计算分析确定。

    ①从失重不致过大考虑。

    与凹形竖曲线的限制条件和计算公式相同，即：

    式中各符号意义同前。

    ②从保证纵面行车视距考虑。

    凸形竖曲线半径过小，路面上凸直接影响行车视距，按规定的视距控制即可推导出计算极限最小半径的公式。 分两种情况：

    a.s≤L，如图4.6所示

    由几何条件

    s＝lw＋lm

    将上述两式代入得：

    图4.6 凸形竖曲线视距（s＜L）

    式中 hw——物高，m，取hw＝0.10m；

    hm——目高，m，取hm＝1.20m；

    lw——竖曲线顶点A距物点的距离，m；

    lm——竖曲线顶点A距目点的距离，m；

    s——要求的行车视距，m，按停车视距考虑；

    L——竖曲线长度，m。

    将hw、hm的值代入式（4.15）并整理得：

    b.s＞L，经推导

    式中 s——要求的视距长度，m；

    ω——纵断面变坡处的坡度角差，计算时取绝对值。

    经比较，式（4.15）和式（4.17）的计算结果比式（4.16）为小，故采用式（4.16）作为标准的制定依据。

    《标准》和《城市道路工程设计规范》规定的各级公路和城市道路的凸形竖曲线的极限最小半径见表4.11和表4.12。

    3）竖曲线一般最小半径

    竖曲线极限最小半径是缓和行车冲击和保证行车视距所必需的竖曲线半径的最小值，该值只有在地形受限制迫不得已时才采用。 通常为了使行车有较好的舒适条件，设计时多采用大于极限最小半径1.5～2.0倍的半径值，此值即为竖曲线一般最小半径。 倍数1.5～2.0，随设计车速减小而取用较大值。 《标准》和《城市道路工程设计规范》规定的竖曲线一般最小半径见表4.11和表4.12。

    （2）竖曲线最小长度

    与平曲线相似，当坡度角较小时，即使采用较大的竖曲线半径，竖曲线的长度也很短，这样容易使司机产生急促的变坡感觉；同时，竖曲线长度过短，易对行车造成冲击。 我国公路按照汽车在竖曲线上3s的行程时间控制竖曲线的最小长度。 《标准》和《城市道路工程设计规范》对竖曲线的最小长度的规定见表4.11和表4.12。

    3.竖曲线设计

    （1）竖曲线设计的一般要求

    竖曲线是否平顺，在视觉上是否良好，往往是构成纵面线形优劣的主要因素。 竖曲线设计应满足以下要求：

    ①宜选用较大的竖曲线半径。 在不过分增加工程量的情况下，宜选用较大的竖曲线半径。通常采用大于竖曲线一般最小半径的半径值，特别是当坡度差较小时，更应采用大半径，以利于视觉和路容美观。 只有当地形限制或其他特殊困难不得已时才允许采用极限最小半径。 在有条件的路段，为获得平顺而连续且视觉良好的纵面线形，可见表4.13选择竖曲线半径。

    表4.13 从视觉观点所需的竖曲线最小半径

    ②同向竖曲线应避免“断背曲线”。 同向竖曲线特别是同向凹形竖曲线间，如直坡段不长，应合并为单曲线或复曲线。

    ③反向曲线间，一般由直坡段连接，也可径相连接。 反向竖曲线间最好设置一段直坡段，直坡段的长度应能保证汽车以设计车速行驶3s的行程时间，以使汽车从失重（或增重）过渡到增重（或失重）有一个缓和段。 如受条件限制也可互相连接或插入短的直坡段。

    ④竖曲线设置应满足排水需要。 若相邻纵坡之代数差很小时，采用大半径竖曲线可能导致竖曲线上的纵坡小于0.3％，不利于排水，应重新进行设计。

    （2）半径的选择

    选择竖曲线半径主要应考虑以下因素：

    ①选择半径应符合表4.11所规定的竖曲线的最小半径和最小长度的要求。

    ②在不过分增加土石方工程量的情况下，为使行车舒适，宜采用较大的竖曲线半径。

    ③结合纵断面起伏情况和标高控制要求，确定合适的外距值，按外距控制选择半径：

    ④考虑相邻竖曲线的连接（即保证最小直坡段长度或不发生重叠）限制曲线长度，按切线长度选择半径：

    ⑤过大的竖曲线半径将使竖曲线过长，从施工和排水来看都是不利的，选择半径时应注意。

    ⑥对夜间行车交通量较大的路段考虑灯光照射方向的改变，使前灯照射范围受到限制，选择半径时应适当加大，以使其有较长的照射距离。