序列相关性的修正

    第三节　序列相关性的修正

    当通过检验，确定模型存在序列相关性时，就不能再用普通最小二乘法估计模型了，而需要寻求新的方法来估计模型。EViews下常用的方法为杜宾两步法与科克伦—奥科特(Cochrane-Orcutt)迭代法。

    下面，继续以4-1为例说明在EViews下如何运用上述方法对序列相关性进行修正。

    一、杜宾(Durbin)两步法

    已知原模型以及其滞后一期模型表达式为

    M_t=α₀+α₁GDP_t+μ_t(4-8)

    M_t－1=α₀+α₁GDP_t－1+μ_t－1(4-9)

    1．自相关的修正

    首先，假定模型存在自相关，即

    μ_t=ρμ_t－1+ε_t　　　　　　(4-10)

    其中，ε_t为满足基本假设的随机误差项。

    将式(4-9)两边乘上ρ，再用式(4-8)减去式(4-9)，得到差分模型

    M_t－ρM_t－1=α₀(1－ρ)+α₁(GDP_t－ρGDP_t－1)+(μ－ρμ_t－1)　　　　　　(4-11)

    变化式(4-11)，得到

    M_t=α₀(1－ρ)+ρM_t－1+α₁GDP_t－α₁ρGDP_t－1+ε_t　　　　　　　　(4-12)

    可见，式(4-12)中的随机干扰项已不再具有序列相关性。因此，需要对模型进行估计，从而求得相关系数ρ的估计量ρ^，输入命令

    ls m c m(－1)gdp gdp(－1)或采用菜单方式，在主菜单下面点击Quick/Estimate Equation，在弹出的对话框(见图4-14)空白处输入

    m c m(－1)gdp gdp(－1)其中，m(－1)，gdp(－1)在EViews下分别表示M_t－1和GDP_t－1。

    

    

    图4-14

    在图4-14中Estimation Setting/Method下选择LS，点击确定，得到图4-15中的估计结果。

    

    

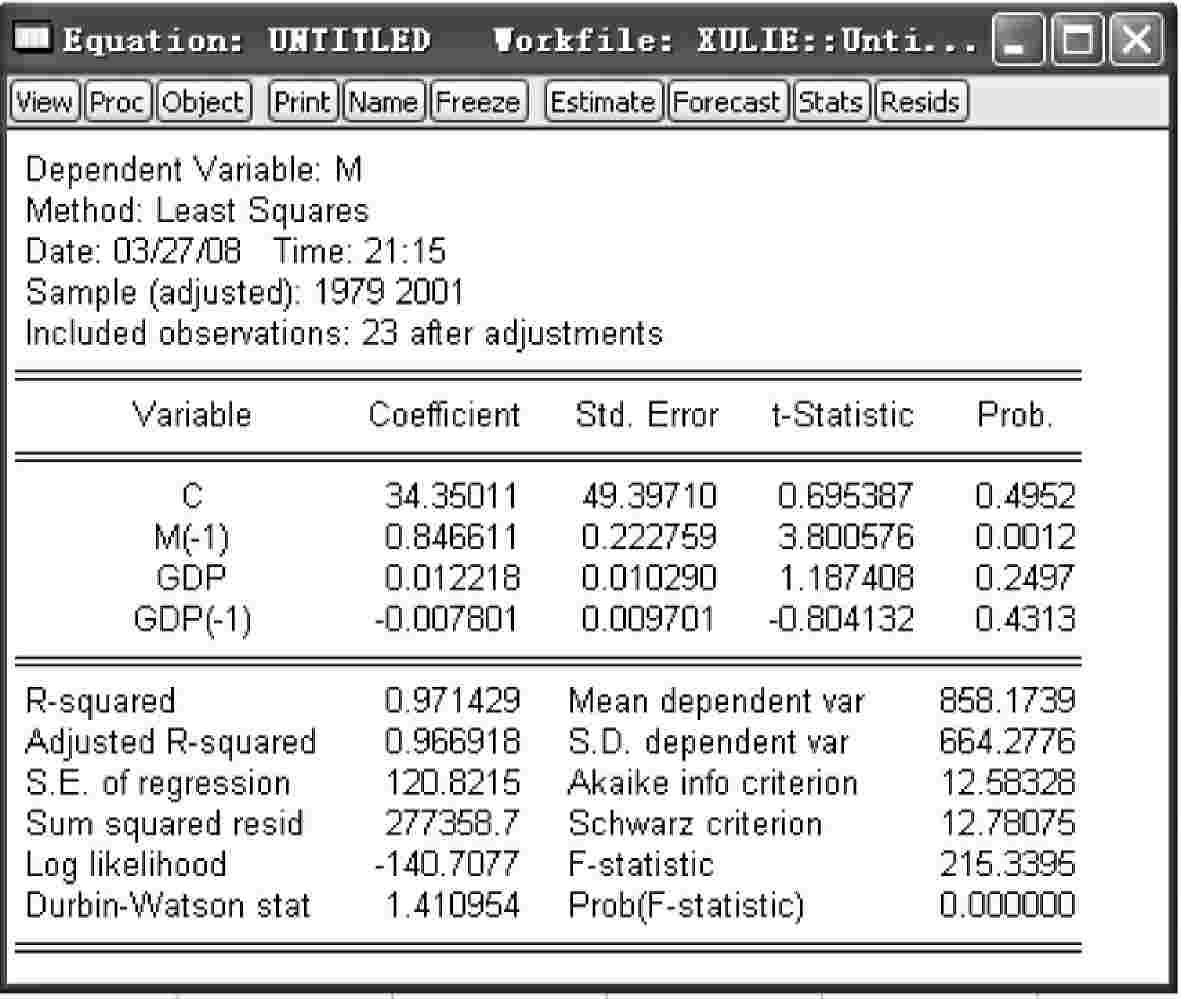
    图4-15

    其中，M(－1)前的系数即为所求的ρ^，ρ^=0．8466。

    用所求得的ρ值带入式(4-11)进行差分变换，在EViews下命令为

    genr im=m－0．8466*m(－1)

    genr ig=gdp－0．8466*gdp(－1)

    其中，im，ig分别为对新序列的命名，得到消除序列相关性的新模型:

    IM_t=β₀+β₁IG_t+ε_t(4-13)估计模型(4-13)，得到回归结果(见图4-16)。

    回归结果中，DW=1．2047，尽管与原模型相比，模型的序列相关性有所改善，然而在5%的显著性水平下(DW=1．27)，仍然认为模型序列相关性没有完全消除，模型随机误差项之间可能存在二阶序列相关。

    2．二阶序列相关的修正

    当随机误差项之间存在二阶序列相关时，即

    μ_t=ρ₁μ_t－1+ρ₂μ_t－2+ε_t(4-14)

    差分模型变为

    

    

    

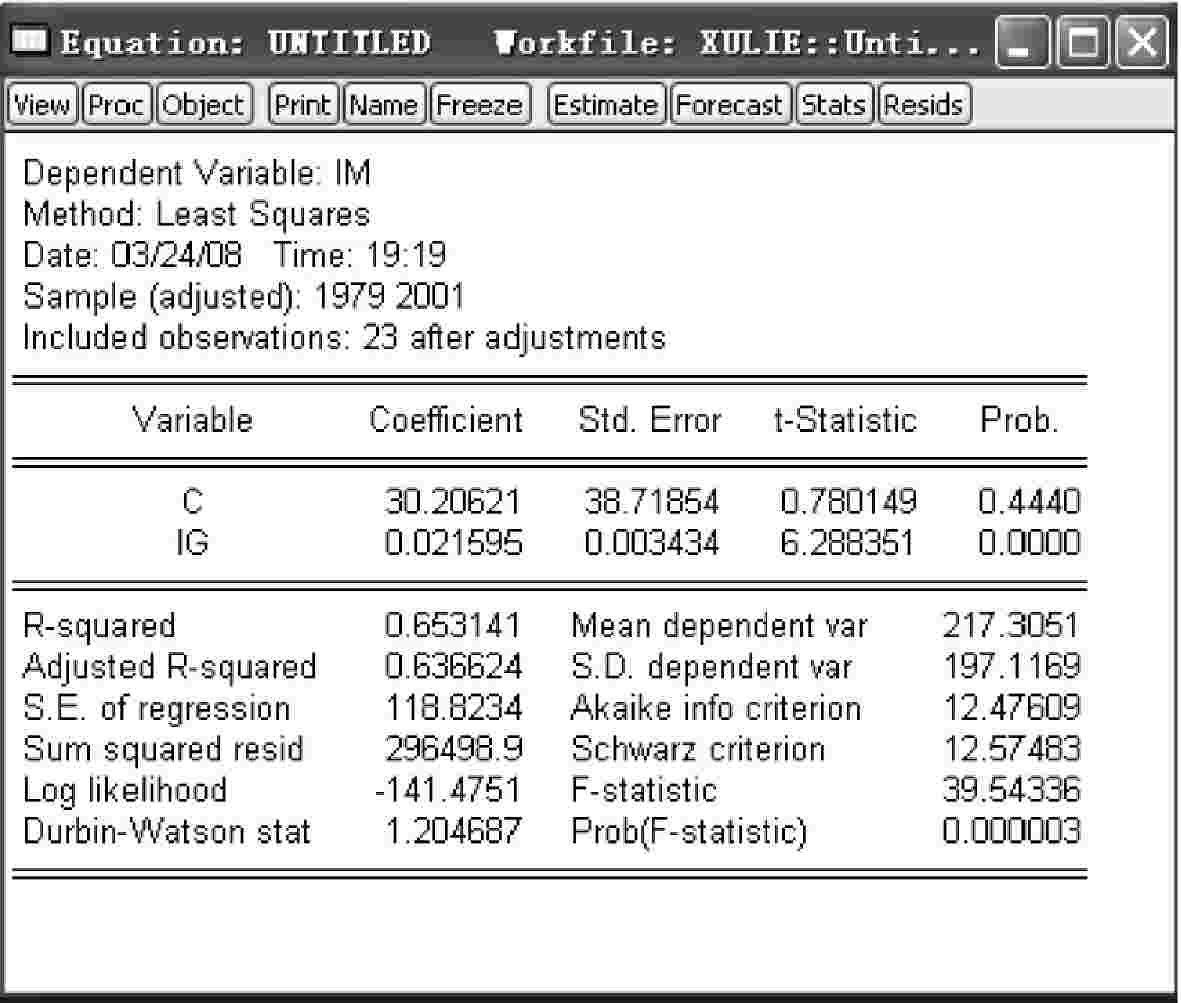
    图4-16

    M_t=(1－ρ₁－ρ₂)α₀+ρ₁M_t－1+ρ₂M_t－2+α₁(GDP_t－ρ₁GDP_t－1－ρ₂GDP_t－2)+(μ_t－ρ₁μ_t－1－ρ₂μ_t－2)(4-15)

    估计模型(4-15)，得到ρ₁，ρ₂的估计量ρ^1，ρ^2，估计命令为

    ls m c m(－1)m(－2)gdp gdp(－1)gdp(－2)

    其中，m(－2)，gdp(－2)分别表示M_t－2，GDP_t－2，估计结果如图4-17所示。因此，ρ^1=0．9382，ρ^2=－0．4687。

    选择EViews主菜单下Quick/Generate Series，在弹出的对话框内分别输入

    iim=m－0．9382*m(－1)+0．4687*m(－2) iig=gdp－0．9382*gdp(－1)+0．4687*gdp(－2)

    如图4-18所示，其中iim，iig为对新序列的命名。

    点击OK，得到新序列iim。值得注意的是，图4-18中上方空白处每次只能输入一个新序列，因此，要创建iig序列，需要重复上述步骤。得到消除二阶序列相关的模型:

    

    

    

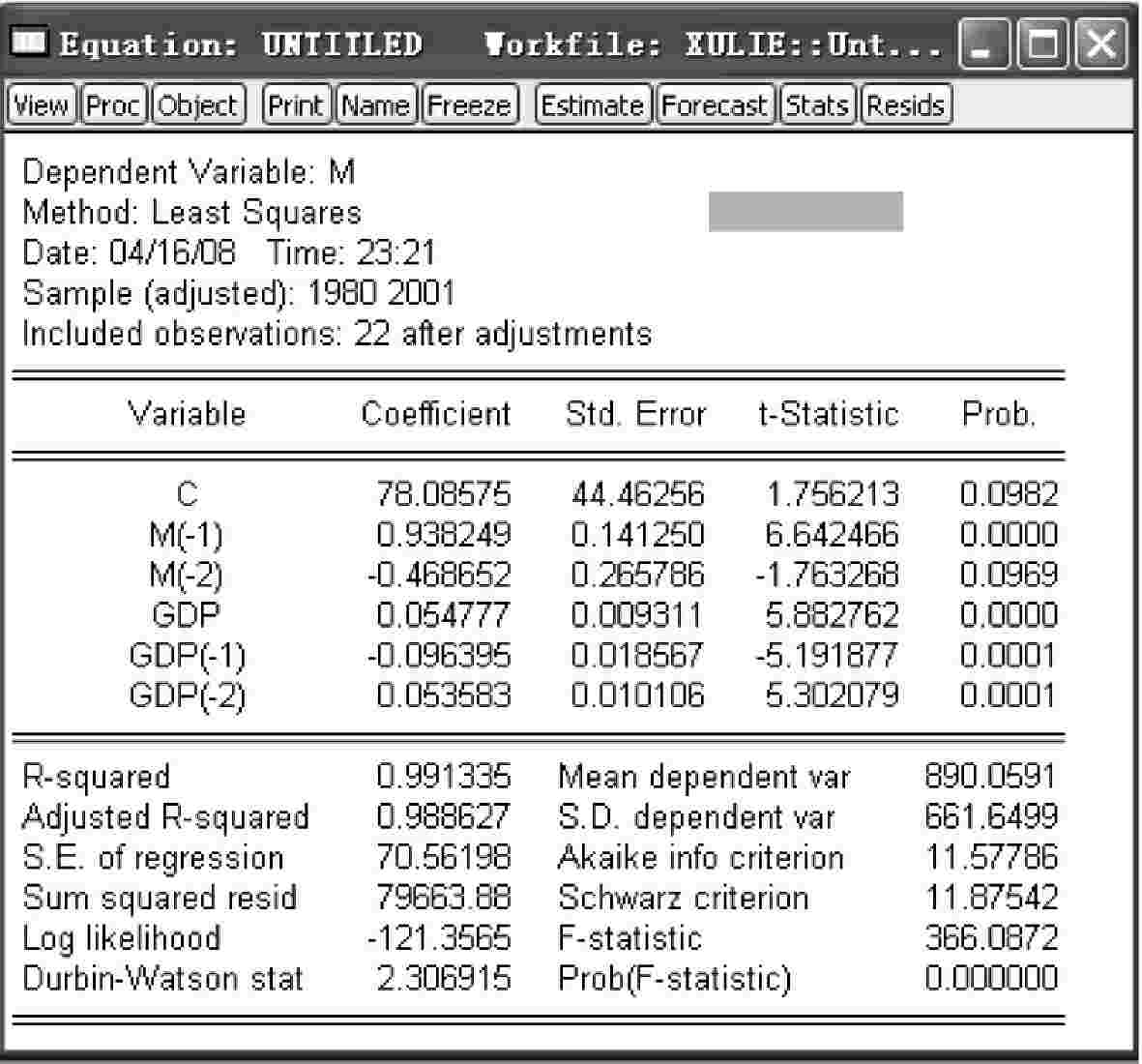
    图4-17

    

    

    图4-18

    

    IIM_t=δ₀+δ₁IIG_t+ε_t(4-16)

    用普通最小二乘法对模型(4-16)进行估计，得到回归结果(见图4-19)。

    

    

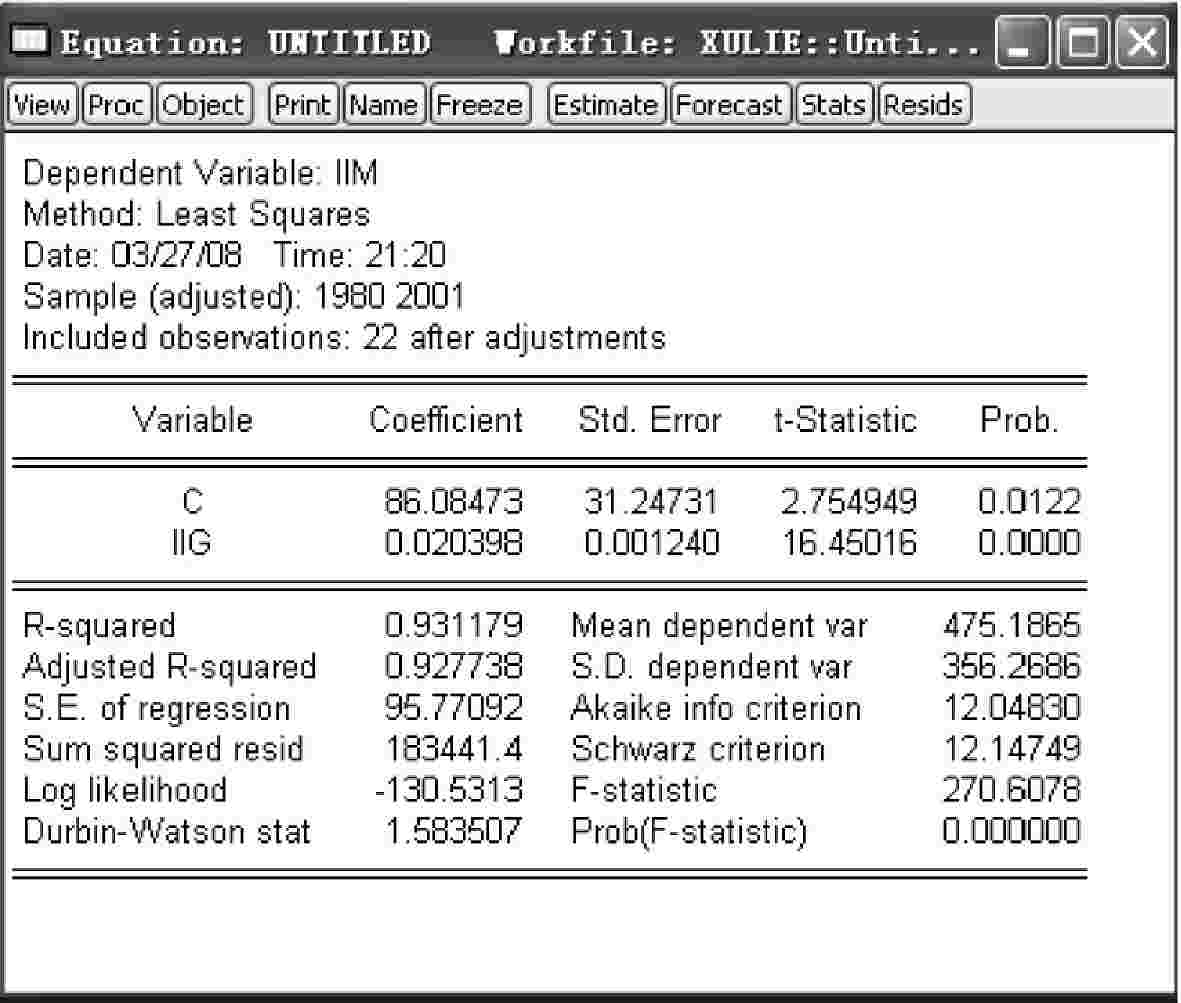
    图4-19

    从图4-19中得出，DW=1．5835，大于5%显著性水平下的临界值，由此可以判断，模型已经消除二阶序列相关性。原模型中，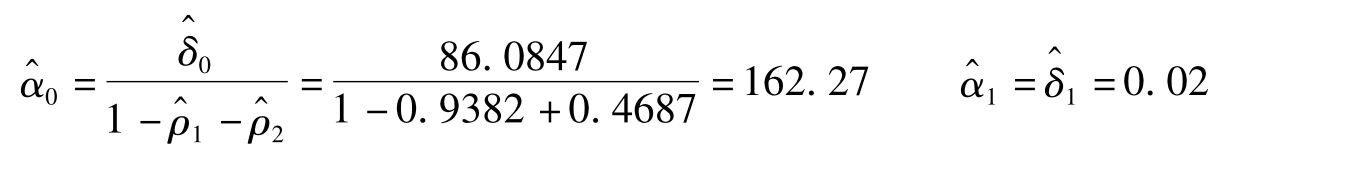

    二、科克伦—奥科特(C-O)迭代法

    在Eviews下，在用普通最小二乘法估计参数时，选择常数项C和GDP以及AR(1)，…，AR(p)作为解释变量，其中AR(p)表示随机误差项的p阶自回归。这样便可以自动完成对ρ₁，ρ₂，…，ρ_p的迭代。在该例中，首先假定模型随机误差项服从自相关，则在命令栏内输入

    ls m c gdp ar(1)

    得到回归结果，如图4-20所示。

    

    

    

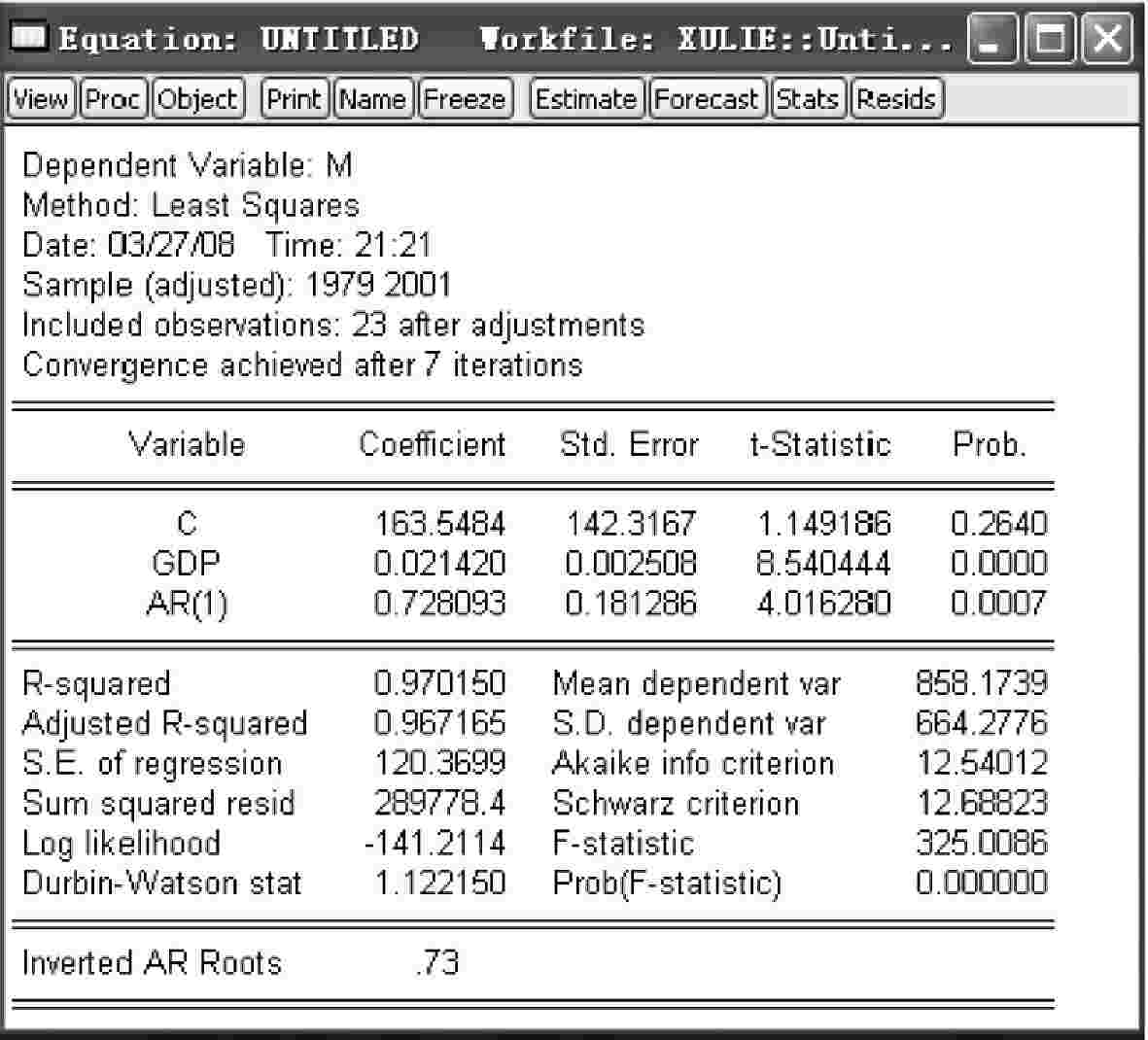
    图4-20

    此时，DW值为1．12，小于5%显著性水平下的临界值，因此，继续选择二阶随机干扰项的自回归项作为解释变量对模型进行估计，在命令栏内输入

    ls m c gdp ar(1)ar(2)

    回归结果如图4-21所示。

    DW值为1．85，大于5%显著性水平下的临界值，此时，模型的序列相关性得到修正。

    三、结果分析

    至此，我们完成了在EViews下对模型的检验与修正，并最终得出中国商品进口方程:

    M^{^}t=162．27+0．02GDP_t(4-17)

    可见，当中国GDP增加一个单位时，将使中国进口增加0．02个单位;中国经济增长对进口的带动作用有限;中国进口量有可能大部分取决于商品进口价

    

    

    

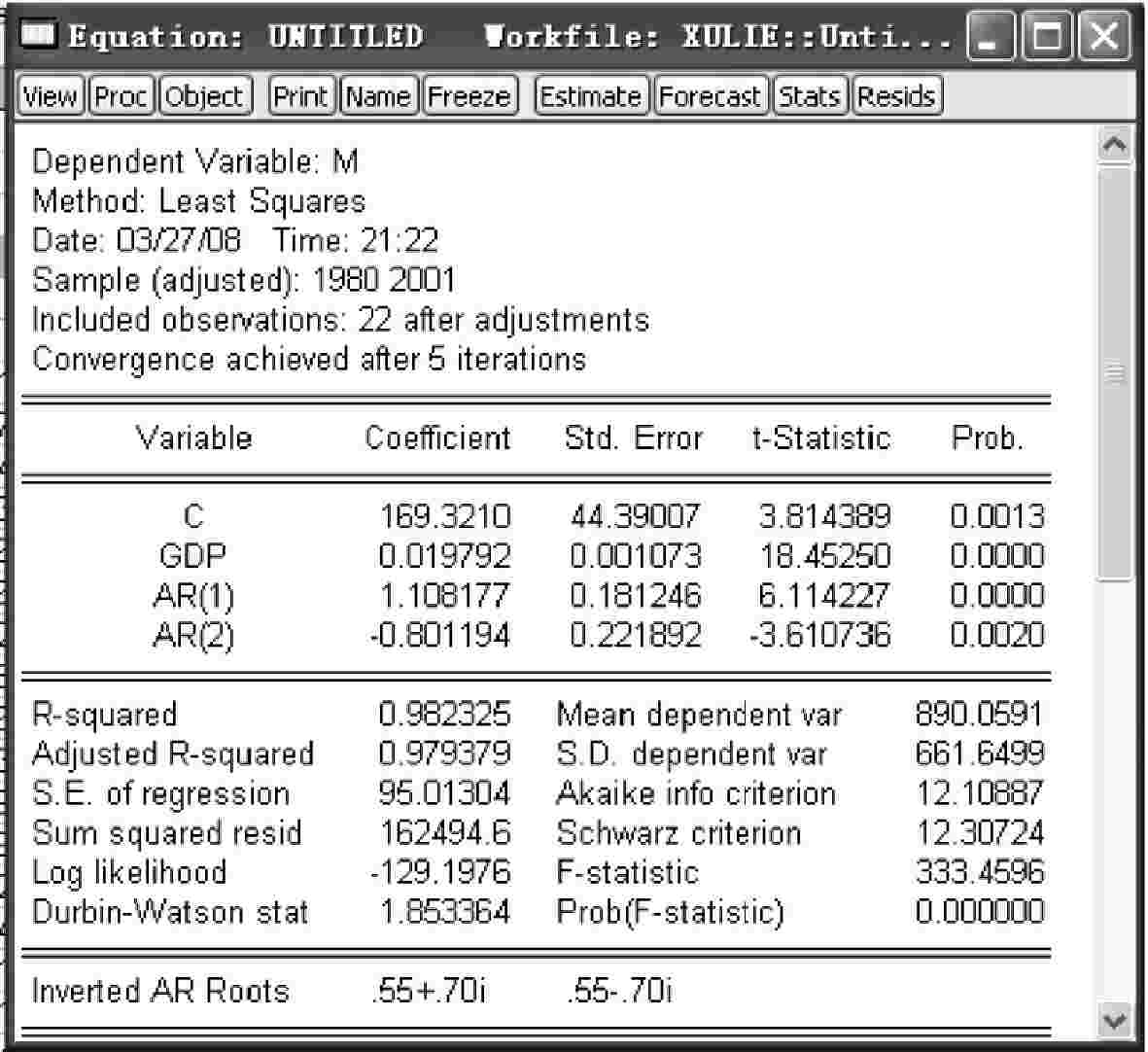
    图4-21

    格指数以及国外商品与国内商品价格指数比。因此，我国要解决当今巨额贸易顺差问题，不仅应大力发展经济，提高人民消费水平，也应该改变国内的经济产业结构，从而带动进口。