
(1/2) 通解的概念
设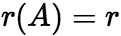 ,
, 为
为 的基础解系,则
的基础解系,则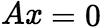 的通解为
的通解为 ,其中
,其中 为任意常数. 如n元线性方程组
为任意常数. 如n元线性方程组 有解,设
有解,设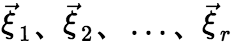 是相应齐次方程组
是相应齐次方程组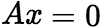 的基础解系,
的基础解系,![]() 是
是 的某个已知解,则
的某个已知解,则![]() 称为非齐次方程组
称为非齐次方程组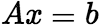 的特解,
的特解,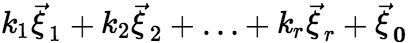 是
是 的通解。 [例题] 解方程组
的通解。 [例题] 解方程组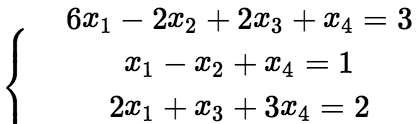 解:对增广矩阵高斯消元化为阶梯形
解:对增广矩阵高斯消元化为阶梯形
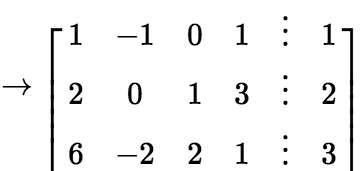

 由
由 ,方程组有解,
,方程组有解,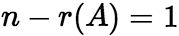 有1个自由变量 先求对应齐次方程组的基础解系,令
有1个自由变量 先求对应齐次方程组的基础解系,令![]() =2,解出
=2,解出 ,所以齐次方程组的通解是
,所以齐次方程组的通解是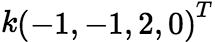 。 再求非齐次线性方程组的特解,令
。 再求非齐次线性方程组的特解,令![]() =0,解出
=0,解出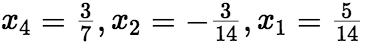 ,特解为
,特解为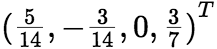 ,所以非齐次方程组的通解是:
,所以非齐次方程组的通解是: +
+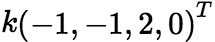
(2/2) 线性方程组解的性质
(1)如果![]() 是
是 的两个解,则
的两个解,则 是
是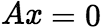 的解。 (2)如果
的解。 (2)如果![]() 是
是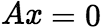 的两个解,则其线性组合
的两个解,则其线性组合 仍是
仍是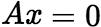 的解。 (3)如果
的解。 (3)如果![]() 是
是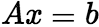 的解,
的解,![]() 是
是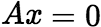 的解,则
的解,则![]() 仍是
仍是 的解。 [例题]:四元方程组
的解。 [例题]:四元方程组 的三个解是
的三个解是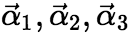 其中
其中 如
如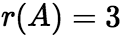 ,则方程组
,则方程组 的通解是_____。 解:
的通解是_____。 解: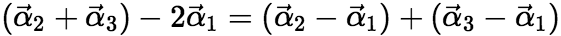
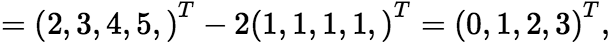 可知
可知 是
是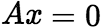 的解。 又秩
的解。 又秩 ,
,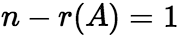 ,所以
,所以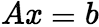 的通解是
的通解是 。
。
上一篇:柏拉图《理想国》导读
下一篇:唯物辩证法的矛盾范畴是什么





.jpg)
.jpg)
