功能原理和机械能守恒定律

    功能原理主要涉及机械能与其他形式能量的转化问题。它的内容是：物体系统的机械能增量等于非保守外力对系统所做的功和系统内耗散力（非保守内力）所做的功的代数和，其本质是能量的转化，系统获得了机械能，就有可能消耗了热能、电能等；反之，如果系统损失了机械能，则就有可能获得热能、电能等形式的能量，但孤立系统总能量不变。如果系统没有非保守力做功，则整个系统没有能量转化，系统机械能守恒。

    一、功能原理的建立背景

    摩擦生热的现象对于我们每个人并不陌生。冬天，人们手冷了都知道两手搓一搓就暖和了，这表明机械运动的能量可以转化为热能。伦福德和戴维的实验进一步证实了这种转化。而在17世纪、18世纪蒸汽机的发明和应用，为热能向机械能的转化做出了令人信服的说明。当然，机械能和热能转化也不都是好的、有用的，机械运动部件之间的运动摩擦耗损不仅消耗机械能，还会损害机械部件，所以常用加机油的方法来避免或者减少这种转化。为了量化这种转化，苏联科学家在动能定理的基础上引入保守内力和非保守内力的概念，因此，内力的功W应包括保守内力的功与非保守内力的功。在前一讲中我们讲到保守内力的功可以用势能的变化表示，进一步把势能和动能合在一起统称为机械能。这样，动能定理的左边就只有非保守力做功了，而右边则是动能和势能之和的变化量（又称机械能的增加量），所以功能原理实际上是动能定理的变形，在运用时应注意：如在考虑机械能时引入了重力势能，由于重力势能属于物体与地球共有，因此物体的重力势能即为内力（保守力）做的功，在计算合外力做功时应剔除重力做功；同样如引入弹性势能，就不应再考虑弹簧的弹力做功。另外，因为功是机械能变化的量度，所以机械能的变化需要通过做功来实现，非保守内力做功则反映系统内部机械能和其他形式能量的转换。特别地，如果系统内有滑动摩擦力时，非保守内力做功为负值，表明系统的一部分机械能转换成了系统的内能。

    二、功能原理和机械能守恒定律的数学表述及物理解析

    1．功能原理

    质点系的功能原理：在质点系运动过程中，外力和非保守内力对系统做的总功等于系统机械能的增量。

    下面我们从动能定理出发来说明功能原理的意义。如果我们用We表示外力对质点系做的总功，Wi表示内力对质点系做的总功，则根据动能定理有

    We+Wi=Ek2-Ek1=ΔEk（11-1）

    进一步将Wi分为保守内力的功WCi和非保守内力的功WNi，上式变为

    We+WCi+WNi=ΔEk（11-2）

    又因保守内力做功可以表示为质点系势能增量的负值，即

    WCi=-（Ep-Ep0）=-ΔEp（11-3）

    将式（11-3）代入式（11-2）并移项可得

    We+WNi=ΔEk+ΔEp=Δ（Ek+Ep）（11-4）

    如果我们定义质点系的动能与势能之和为质点系的机械能，并用E表示，即E=Ek+Ep，则式（11-4）可改写为

    We+WNi=ΔE（11-5）

    式（11-5）就是功能原理的数学表达式，它表明在质点系运动过程中任一位置，外力和非保守内力对系统做的总功等于系统机械能的增量。

    2．机械能守恒定律

    在式（11-5）中，如果满足We=0，WNi=0，则

    ΔE=0（11-6）

    式（11-6）是机械能守恒定律的数学表达式。也就是说，孤立系统在外力和非保守内力做功皆为零的情况下，系统机械能保持不变，这叫机械能守恒定律。当然式（11-6）也可以改写为

    Ek+Ep=恒量 （11-7）

    三、应用举例

    例1 如图11-1所示，一条质量均匀分布的铁链，总质量为m，总长为l，一段放在水平桌面上与桌面摩擦系数为μ，另一段悬挂在桌子边缘。一人慢慢移动悬挂段，问：（1）悬挂段长度a为多少时铁链开始下滑？（2）金属链全部离开桌面时速度为多少？

    图11-1

    解：当下垂部分重力等于摩擦力时链条开始下滑，即

    时铁链将开始下滑。解（11-8）式可得

    要计算链条全部离开桌面的速度，根据功能原理，需要首先计算外力摩擦力做功。以链条下垂位置为坐标原点，建立如图11-1所示坐标。链条下落任一x距离时，摩擦力可表为

    在链条从下垂a位置到全部下落，摩擦力做的功可写为

    根据功能原理，并选取桌面为重力势能零点，则有

    Wf=ΔE（11-12）

    即

    将式（11-9）代入式（11-13）解得

    例2 计算第一宇宙速度

    解：第一宇宙速度是指从地面发射物体（卫星），使其在地面附近（离地面的高度与地球半径相比很小）轨道绕地球飞行所需要的最小发射速度，通常用v1表示。在不考虑空气阻力影响时，发射物与地球组成的系统满足机械能守恒。假设地球半径为R，质量为M，发射物质量为m，地面发射时速度为v1，在离地球高h绕地球做匀速圆周运动时速度为v，根据机械能守恒定律有

    因万有引力提供卫星绕地球做圆周运动的向心力，有

    联立式（11-15）和式（11-16）可以解得

    考虑到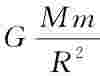=mg可得

    将式（11-18）代入式（11-17）中有

    如果假设h≪R，R≈6．37×106m，则

    也就是说，从地面上发射人造卫星的最小发射速率为7．9×103m／s。考虑到空气阻力，火箭壳、燃料等本身的质量，实际所需要的速度要大于这个值。

    四、课后习题

    11-1 如图11-2所示，一个木块沿倾角θ=30°的斜面从初始位置以初速度v0=4．5m／s向上运动。已知木块与斜面之间的摩擦系数为μ=0．35，以木块初始位置为重力势能零点，试求木块动能等于重力势能处相对其初始位置的高度。

    图11-2

    11-2 一轻弹簧的一端固定在一斜面的底端，另一端与质量为m的物块相连。初始时刻物块处在离弹簧原长-x0的A位置（沿斜面），如果在一外力作用下，物块由A点沿斜面向上缓慢移动了3x0距离到达B点，求这个过程中外力所做的功。

    11-3 如图11-3所示，Γ形刚性支架固连在面积足够大的木板上，木板放在水平桌面上，其与桌面的摩擦系数为μ，木板与支架的总质量为M。长度为l质量为m的均质细杆可以绕支架顶端轴自由旋转。现将细杆拉到水平位置后由静止释放，在细杆下摆过程中假设木板不移动。当细杆摆至竖直位置时，与固连在木板上的不计质量的小木块A发生完全非弹性碰撞。求：

    图11-3

    （1）细杆摆至竖直位置时的角速度的大小；

    （2）释放细杆瞬间地面受到的压力；

    （3）碰撞后系统相对地面移动的最大距离。