简单模型的实证分析

    

    根据前面几节的讨论，我们知道简单ACD模型的形式为：

    

    式中，xi＝ti－ti－1是两个事件发生时间之间的间隔，条件期间过程ψi＝E（xi｜Ωi－1）为第i个期间持续的期望，Ωi－1包括了时刻ti－1时所有的有用信息集。｛εi｝～i.i.d并且E（εi）＝μ，VAR（εi）＝σ。

    简单ACD模型的对数变形则为：

    类型Ⅰ

    类型Ⅱ

    下面我们用中国石化（600028）2004年2月1日至2004年4月30日期间的实时交易数据估计简单ACD模型以及对数线性ACD模型。定义中国石化价格期间为价格累计变化0.03元以上的时间间隔，交易时间每天包括早晨9∶30～11∶30、下午1∶00～3∶00，隔夜以及休市时的时间间隔被剔除。时间间隔消除了日内效应。

    我们用极大似然法来估计上式中的简单ACD模型以及对数线性ACD模型，我们假设εi∈i.i.d且具有Burr密度：

    

    κ＞γ＞0，Burr密度包括Weibull（γ→0）、指数（γ→0且k＝1）和对数逻辑（γ→1）分布。

    （9-9）式的实证结果为：

    

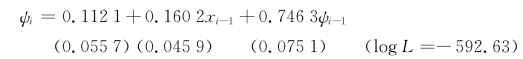
    （9-10）式的实证结果为：

    

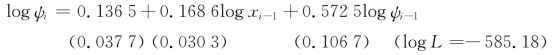
    （9-11）式的实证结果为：

    

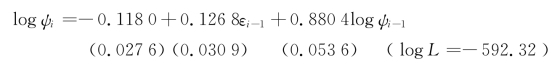
    这里我们列举了国内在ACD模型实证研究方面的成果，刘勤（1999）^[6]模拟的简单ACD模型（εi具有指数密度）为：

    

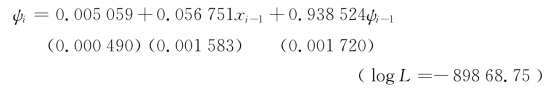
    张国勇（2004）模拟的简单ACD模型以及对数线性ACD模型为：

    

    由于我们假设εi具有Burr密度分布，估计结果与εi具有指数分布的情况会有些差异。所有模型实证结果参数都是显著的，εi具有Burr密度的模型其极大似然值的绝对值更小。