
4.1.1 马尔科维茨均值—方差模型
投资者需要承担的风险多种多样,如坏债风险、利率风险、市场风险、购买力风险、流动性风险、政治风险和管理风险等。投资经验表明,通过持有多样化的资产组合可以分散和降低风险。1952年,现代资产组合理论的创始人—马尔科维茨(Harry Markowitz)提出了均值—方差模型。该模型提供了一种科学的风险分析方法,所以又被称为马尔科维茨风险分散模型。所谓均值表示投资的预期收益,所谓方差是指收益的方差,表示风险。马尔科维茨假设所选择各项资产的风险不完全正相关,即资产类别相关性较低甚至相反。投资者的资产完全用来投资,不存在借入和借出,通过均值—方差模型可以在所选的资产中求解有效率的资产组合。
如图4-1所示,曲线XY是所有有效率的资产组合的集合,也可称之为有效边界或效率边界,表示有效率的风险与回报的替换关系。P或N等有效边界上的任何一点都可以在给定的风险条件下获得最大的预期回报,而边界之外的点如M均属于无效率的资产组合,它要么在给定风险下所得回报较小(M与N相比),要么在给定回报下所承担的风险较大(M与P相比),因此这类资产组合应该避免。实际计算过程要求估计出预期回报与风险等输入变量,计算结果可以得出给定风险下预期回报最大或给定预期回报收益水平下风险最小的资产组合,最终构成预期回报与风险坐标中的有效边界。
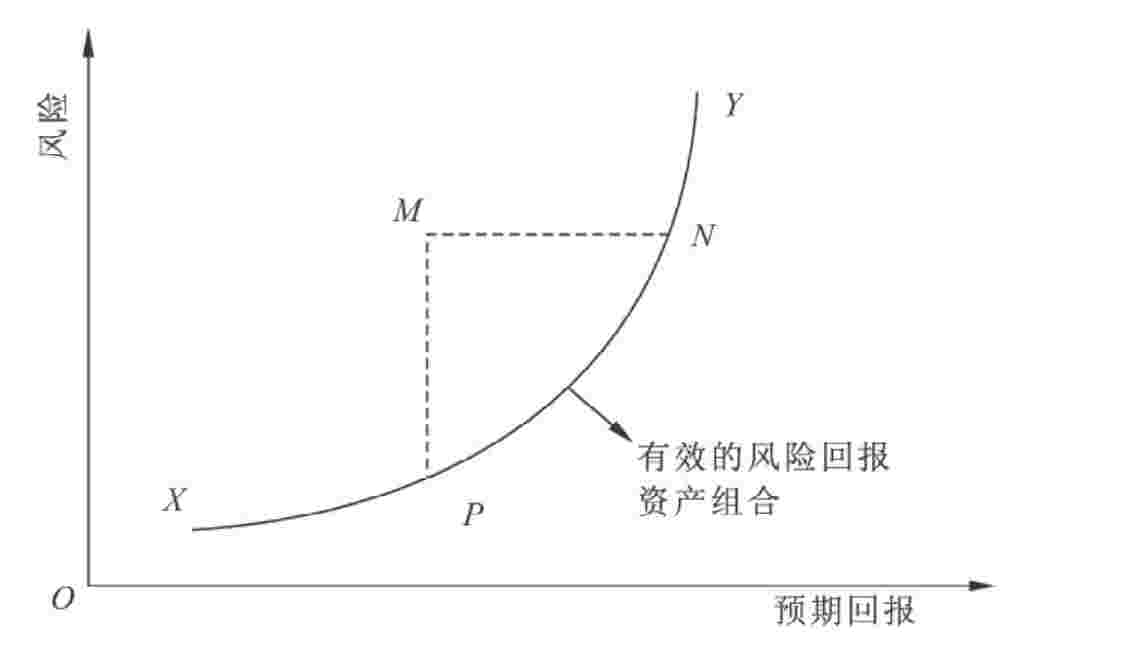
图4-1 马尔科维茨风险分析模型(Mean Variance Model)
资料来源:Harry Markowitz.Portfolio Selection[J].The Journal of Finance,Vol.7,No.1,Mar 1952,P82.
事实上,资本市场除了风险资产,还有某些无风险资产,如流动性强、限期少于一年的国库券、商业票据等。1958年,托宾(James Tobin)将无风险资产引入均值—方差模型。托宾的研究显示,在一个投资组合内既可包括有风险资产,也可包括无风险资产。持有风险资产虽然可能获得收益,但要承担由此产生的风险。投资收益带来的正效用会随着收益的增加而递减,而风险的负效用会随着风险的增加而递增,当最后一单位安全资产所产生的边际正效用与最后一单位风险资产所产生的边际负效用之和为零时,投资者的总效用达到最大。因此,资产组合环节应包括两个步骤:一是根据均值方差模型决定投资于不同风险资产的比例;二是在风险资产与安全资产之间做出分散投资的决策。马尔科维茨与托宾为现代资产组合理论奠定了良好的基础。马尔科维茨提出的均值—方差模型有一定的前提,即假设投资者无资金借入和借出,但是这一前提条件并不现实。而托宾的研究需要使用市场各类资产的预期收益、标准差及两两资产间的协方差,计算工作量巨大,可操作性不强。





.jpg)
.jpg)
