
形同质异———二次曲线的切线及切点弦
张思意
近几年高考中,常考查二次曲线的切线及切点弦,不少同学对此感到很困难。本文将二次曲线的切线及切点弦做出探索,希望能更好地对这个知识点有整体的认识及把握,从而能更好地解决这类问题。
一、圆的切线及切点弦
(一)过圆上一点的切线
已知圆(x-a)2+(y-b)2= r2上一点P(x0,y0),则过P点的圆的切线方程为:(x0-a)(x-a)+(y0-b)(y-b)= r2。特别地:当圆的方程为x2+ y2=1时,切线方程是x0 x+ y0 y= 1
1.(2009年全国)已知圆O:x2+ y2= 5和点A(1,2),则过A且与圆O相切的直线与两坐标轴围成的三角形的面积等于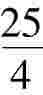 __。
__。
解析:∵A(1,2)在圆x2+ y2=5上,
∴过A点与⊙O相切的直线方程为x+2y=5,与坐标轴交点为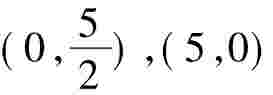 。
。
![]()
2.(2010年广东模拟)过单位圆x2+ y2=1是位于第一象限的任意一点作圆的切线,则该切线与两坐标轴所围成的三角形面积的最小值是__
解:设切点坐标为(x0,y0),则切线方程为xx0+ yy0= 1,该切线与两坐标轴的交点坐标分别是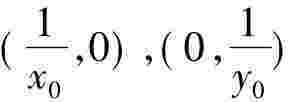 ,故切线与两坐标轴所围成的三角形的面积是
,故切线与两坐标轴所围成的三角形的面积是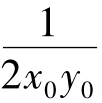 ,又
,又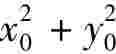 =1,故
=1,故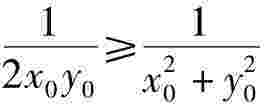 =1,即切线与两坐标轴所围成的三角形面积的最小值是1。
=1,即切线与两坐标轴所围成的三角形面积的最小值是1。
3.(2009年江西改编)设直线系M:x cosθ+(y-2)sinθ=1(0≤θ≤2π),则下列命题中是真命题的个数是( C)
①存在一个圆与所有直线相交 ②存在一个圆与所有直线不相交
③存在一个圆与所有直线相切 ④M中所有直线均经过一个定点
⑤存在定点P不在M中的任一条直线上
⑥对于任意整数n(n≥3),存在正n边形,其所有边均在M中的直线上
⑦M中的直线所能围成的正三角形面积都相等
A.3 B.4 C.5 D.6
解析:M为圆C:x2+(y-2)2=1的全体切线组成的集合,所以存在圆心在(0,2),半径大于1的圆与M中所有直线相交,也存在圆心在(0,2),半径小于1的圆与M中所有直线均不相交,也存在圆心在(0,2),半径等于1的圆与M中所有直线相切,所以①②③⑤⑥正确
(二)圆的切点弦
(1)定义:已知圆(x-a)2+(y-b)2= r2,圆外一点P(x0,y0),则过P点可做圆的两天切线PA、PB,切点分别为A、B则线段AB称为圆的切点弦,直线AB称为圆的切点弦方程。
(2)推导:设A(x1,y1)、B(x2,y2)由圆的切线知识可知:
直线PA、PB的方程分别是
(x1-a)(x-a)+(y1-b)(y-b)= r2
(x2-a)(x-a)+(y2-b)(y-b)= r2
因P(x0,y0)在两直线上,所以有
(x1-a)(x0-a)+(y1-b)(y0-b)= r2
(x2-a)(x0-a)+(y2-b)(y0-b)= r2
由两点确定直线得直线AB得方程为:(x0-a)(x-a)+(y0-b)(y-b)= r2。
特别地:当圆的方程为x2+ y2=1时,切点弦所在直线方程是x0 x+ y0 y=1。
这与前面得到的圆的切线方程外形一致。真是“形同质异”。下面我们看看切点弦知识的运用。
若椭圆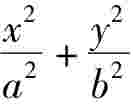 =1的焦点在x轴上,过点
=1的焦点在x轴上,过点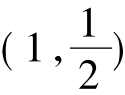 作圆x2+ y2= 1的切线,切点分别为A,B,直线AB恰好经过椭圆的右焦点和上顶点,则椭圆方程是。
作圆x2+ y2= 1的切线,切点分别为A,B,直线AB恰好经过椭圆的右焦点和上顶点,则椭圆方程是。
这是高考中填空题最难的一题了。我们应用两种不同的方法看看。
方法一:应用切点弦知识很快可以得到:直线AB方程为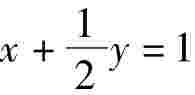 .代入P(c,0)、Q(0,b)得c= 1,b= 2.根据公式
.代入P(c,0)、Q(0,b)得c= 1,b= 2.根据公式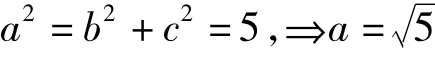 ,即椭圆方程为:
,即椭圆方程为: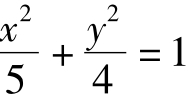
方法二:设过点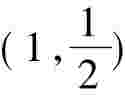 的直线方程为:当斜率存在时,y= k(x-1)+
的直线方程为:当斜率存在时,y= k(x-1)+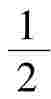 ,根据直线与圆相切,圆心(0,0)到直线的距离等于半径1可以得到k=
,根据直线与圆相切,圆心(0,0)到直线的距离等于半径1可以得到k=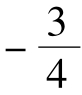 ,直线与圆方程的联立可以得到切点的坐标
,直线与圆方程的联立可以得到切点的坐标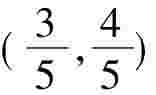 ,当斜率不存在时,直线方程为:x= 1,根据两点A:(1,0),B:
,当斜率不存在时,直线方程为:x= 1,根据两点A:(1,0),B: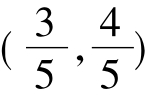 可以得到直线:2x+ y-2= 0,则与y轴的交点即为上顶点坐标(2,0)→b=2,与x轴的交点即为焦点→c= 1,根据公式
可以得到直线:2x+ y-2= 0,则与y轴的交点即为上顶点坐标(2,0)→b=2,与x轴的交点即为焦点→c= 1,根据公式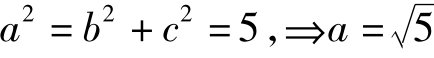 ,即椭圆方程为:
,即椭圆方程为: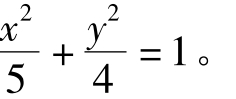
比较以上两种方法不难看出方法一的巧妙之处!
二、圆锥曲线的切线及切点弦
在圆锥曲线中是否有相同的结论呢?应用高等数学中“隐函数”求导的知识来进行研究:
(一)推导过圆锥曲线上一定点的切线
设P(x0,y0)是椭圆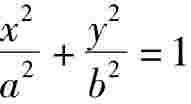 上一点,则过P点的椭圆的切线方程的求法:
上一点,则过P点的椭圆的切线方程的求法:
解:求导得: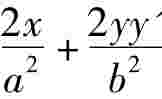 =0,所以斜率k= y'=
=0,所以斜率k= y'=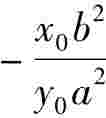 ,所以切线方程为:y-y0=
,所以切线方程为:y-y0=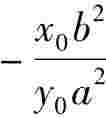 (x-x0)。又由
(x-x0)。又由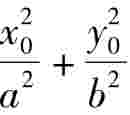 = 1,化简得:
= 1,化简得: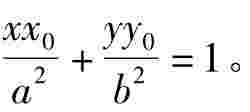
同理可得: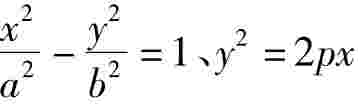 的切线分别是:
的切线分别是: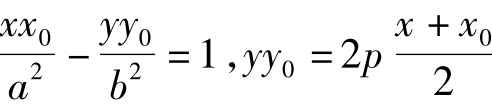
归纳:(1)过二次曲线的上一点的切线规律:二次项的一个因子中x、y分别换做定点的横纵坐标,一次项用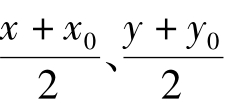 分别代替。
分别代替。
(2)应用圆的切点弦方程求法容易得到: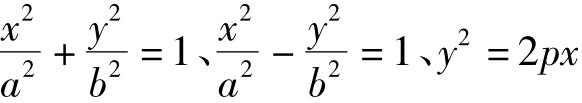 的切点弦分别是:
的切点弦分别是: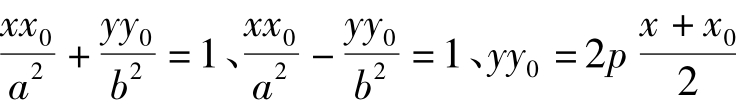 。这又是一组“形同质异”。
。这又是一组“形同质异”。
我们看看这一知识点的应用
(2008江西)设点P(x,y)在直线x=m(y≠±m,0<m<1)上,过点P作双曲线x200-y2= 1的两条切线PA、PB,切点为A、B,定点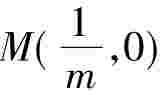 。
。
(1)求证:A、M、B三点共线。
方法一:由切点弦方程可知,直线A、B的方程为:mx-y0 y= 1。定点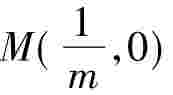 .显然在直线AB上,所以A、M、B三点共线。
.显然在直线AB上,所以A、M、B三点共线。
方法二:设A(x1,y1),B(x2,y2),由已知得到y1 y2≠0,且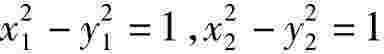 ,
,
(2)设切线PA的方程为:y-y1= k(x-x1)由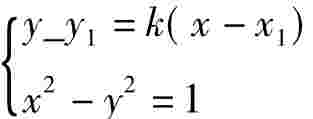 得
得
(1-k2)x2-2k(y1-kx1)x-(y1-kx1)2-1= 0
从而Δ=4k2(y1-kx1)2+ 4(1-k2)(y1-kx1)2+4(1-k2)= 0,解得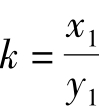
因此PA的方程为:y1 y= x1 x-1
同理PB的方程为:y2 y= x2 x-1
又P(m,y0)在PA、PB上,所以y1 y0=mx1-1,y2 y0=mx2-1。
即点A(x1,y1),B(x2,y2)都在直线y0 y=mx-1上
又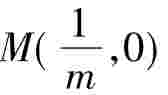 也在直线y0 y=mx-1上,所以A、M、B三点共线
也在直线y0 y=mx-1上,所以A、M、B三点共线
在这里又一次可以看到应用切点弦知识在解决问题时的简洁!
我们在新课标的教学和学习过程中,应更注重对知识本质的把握。对数学概念内涵及外延做适当的拓展,有利于从整体上认识其本质。利用高等数学知识理解和认识初等数学中的概念,也是中学一线教师践行新课标的必备素质!
上一篇:“应交增值税明细表”编制举例
下一篇:客户关系管理的定义与内涵





.jpg)
.jpg)
