随机变量的方差与样本方差

    1.7.5　数理统计的基本概念

    数理统计是随机数学的一个分支.它以概率为基础，给出处理随机性产生的数据的原理与方法.数理统计的内容很多，读者对此仅需初步了解.

    1.总体与样本

    总体是全体研究对象的某个特征值;样本是总体中部分个体的该特征值.

    数理统计的基本内容是:如何根据样本所提供的信息对总体中的未知量作统计推断。

    样本具有双重意义.随机抽样前，样本X₁，…，X_n是n个随机变量;随机抽样后，样本表现为n个数据x₁，…，x_n，这n个数据也称为样本值.在不致引起误解时，样本值也简称为样本.

    总体用随机变量X表示，因为总体反映的特征值带有随机性，当总体X服从正态分布时，称X为正态总体.

    今后常用“X₁，…，X_n是取自总体X的容量为n的样本”这类语言.这句话的含义是:X₁，…，X_n是相互独立的随机变量，且每一个X_i都与总体X的分布相同，i=1，…，n.当总体X是离散型随机变量时，每一个X_i与X的概率分布相同;当总体X是连续型随机变量时，每一个X_i与X的概率密度函数相同.

    对于每一个i=1，…，n，X_i与X同分布蕴含了它们的数学期望、方差与标准差都相等，即

    E(X_i)=E(X)，D(X_i)=D(X).

    2.统计量

    样本X₁，…，X_n的函数统称为统计量.统计量不能带有总体X中任何未知量.

    以下给出数理统计中常用的统计量:

    ①样本均值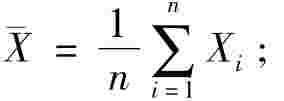

    ②样本方差S²=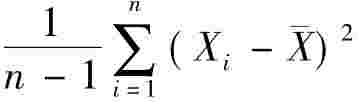，样本标准差S=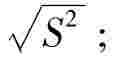

    ③样本k阶原点矩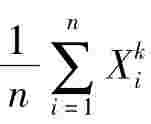，样本k阶中心矩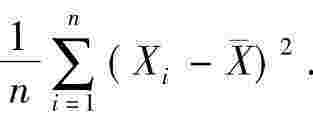

    样本均值是样本一阶原点矩，但样本方差不是样本二阶中心矩.

    定理3设X₁，…，X_n是取自总体X的容量为n的样本.已知E(X)=μ，D(X)=σ²，那么:

    ①E(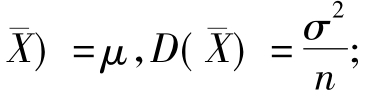

    ②E(S²)=σ².

    这里要注意，E(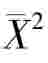)≠μ²，E(S)≠σ.

    3.三个常用分布

    χ²分布、t分布与F分布是数理统计中经常使用的连续型随机变量的分布，读者不必关心它们的概率密度函数，但要知道它们的参数，这些参数都称为自由度.

    设X₁，…，X_n相互独立，且每一个X_i都服从标准正态分布N(0，1)，则χ²=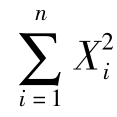服从自由度为n的χ²分布，记作χ²(n).

    设随机变量X与Y相互独立，且X～N(0，1，)，Y～χ²(n)，则T=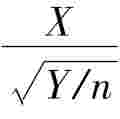服从自由度为n的t分布，记作t(n).

    设随机变量X与Y相互独立，且X～χ²(n₁)，Y～χ²(n₂)，则F=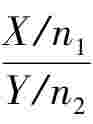服从自由度为(n₁，n₂)的F分布，记作F(n₁，n₂).

    今后经常要用到χ²分布、t分布与F分布的临界值.这些临界值都可以通过查表解决.

    定理4设X₁，…，X_n是取自正态总体N(μ，σ²)的容量为n的样本.

    

    

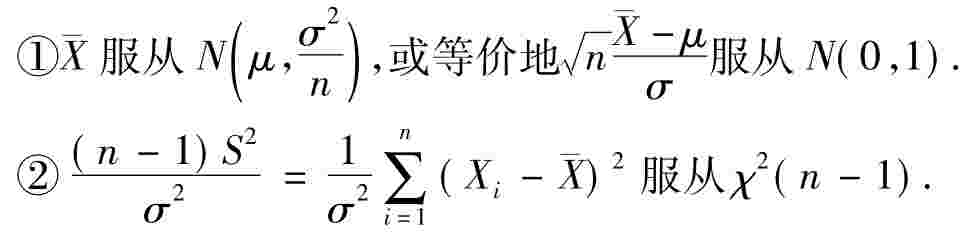
    定理5设X₁，…，X_n1是取自正态总体N(μ₁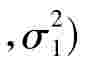的容量为n₁的样本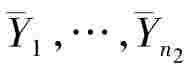是取自正态总体N(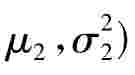的容量为n₂的样本.样本均值与样本方差分别记作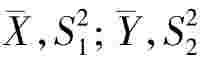，那么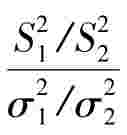服从F(n₁－1，n₂－1).

    定理6在定理5中，再假定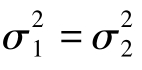，那么，

    

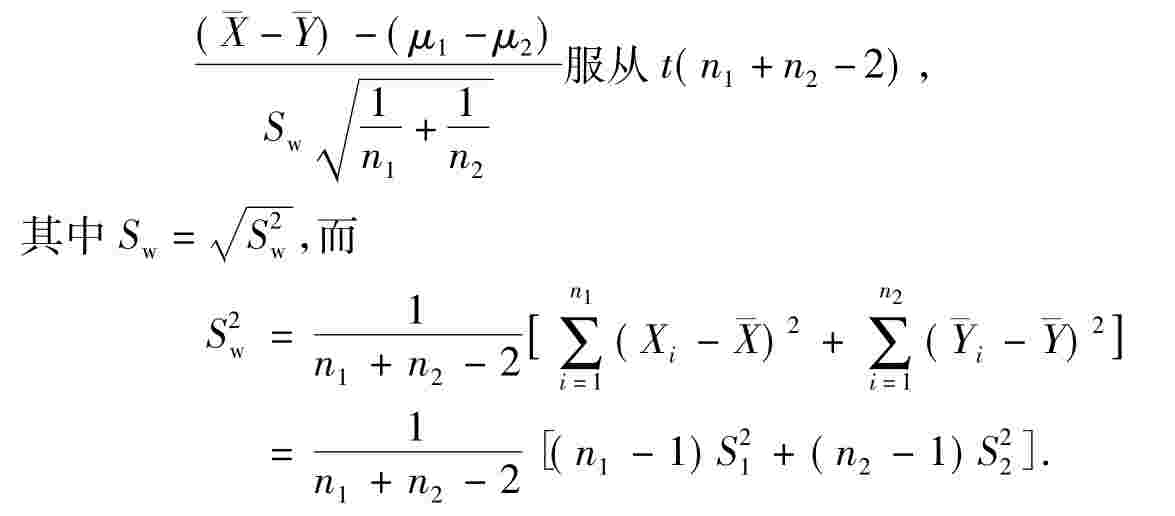
    【例1.7-31】设X₁，…，X_n是取自总体X的容量为n的样本.已知X服从区间(－θ，θ)上的均匀分布.试求E(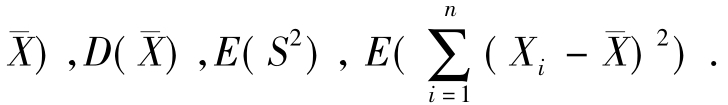

    解:已知区间(－θ，θ)上的均匀分布的数学期望与方差分别是

    

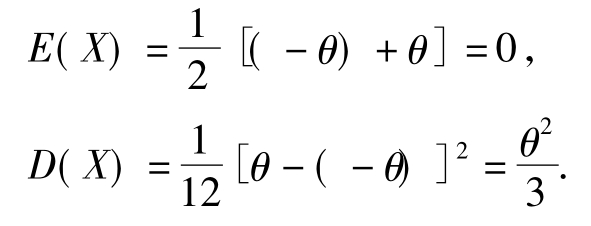
    按定理3，则

    

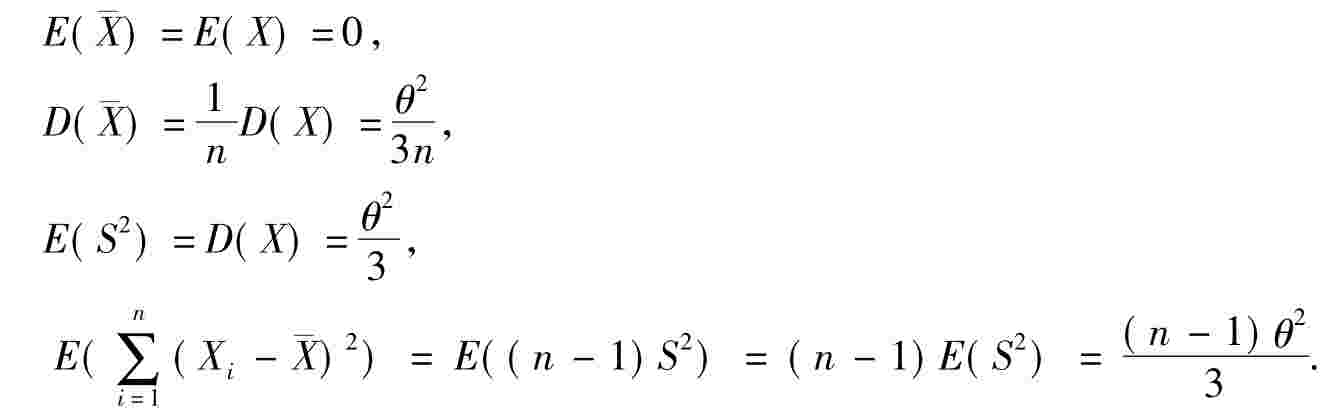
    【例1.7-32】设X₁，…，X₁₆是取自正态总体N(0，σ²)的样本，则(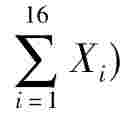

    

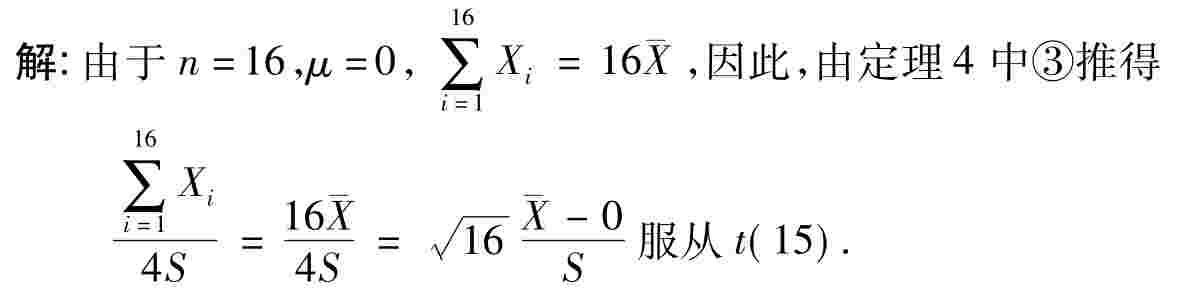
    /4S服从(　).

    (A)正态分布　　　(B)自由度为16的t分布

    (C)标准正态分布　(D)自由度为15的t分布故选(D).

    【例1.7-33】设X～N(0，1)，则X²服从(　).

    (A)χ²(n)　(B)χ²(1)　(C)t(1)　(D)N(0，1)

    解:在χ²分布定义中取n=1，得X²～χ²(1).故选(B).