
精确线性化是通过严格的状态变换与反馈变换进行的,变换的过程中没有忽略任何高价非线性项,因而线性化的过程精确的,而不是借助于动态系统的线性近似[253]。
选取状态变量X=[x1,x2,x3,x4]=[δ,ω,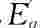 q,Xc],式(5-81)可表示为双输入双输出放射非线性系统的形式如下
q,Xc],式(5-81)可表示为双输入双输出放射非线性系统的形式如下
式中:x=(x1,x2,x3,x4)T=(δ,ω,E′q,Xc)T;g1=(001/Td00)T;g2=(0001/TC)T;y=(y1y2)T=(h1h2)T;u1=uf;u2=uc;y1=h1=δ;y2=h2=Pe;
f(x)=[f1(x)f2(x)f3(x)f4(x)]T=
要想对式(5-83)实现精确反馈线性化,需对其进行验证,即判断系统的相对阶。为此,对公式(5-83)的输出h1,h2计算各阶李导数,如下
该控制系统的自由阶集合r= r{r1,2}={3,1},且r=r1+r2=4,即系统的自由阶总数等于其阶数,所以精确线性化有解。
又有
式中,J11=Lg1L2fh1,J12=Lg2L2fh1,J21=Lg1L0fh2,J22=Lg2L0fh2。显然J(x)≠0,故矩阵J(x)为非奇异矩阵。为此,可以求出以下坐标变换Z=φ(x)为
将式(5-85)化为Brunovsky标准型,即
系统输出方程为
则系统可写成
V=[v1v2]T;Z=[z1z2z3z4]T;Y=[y1y2]T。
为此,构造的状态反馈为
取L1=L3fh1(x),L2=L1fh2(x),则
其中,k1=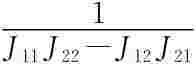
上一篇:节日风俗的发展与演变
下一篇:文斗非洲绿巨“螳螂”





.jpg)
.jpg)
