
5.3 误差传播定律
上一节中,已经阐述了衡量一组观测值质量的精度指标,并已指出,通常采用的精度指标是中误差。但在实际测量工作中,往往会遇到某些量的大小不是直接测定的,而是由观测值通过一定的函数关系计算出来的,即常常遇到的某些量是观测值的函数。例如,水准测量中,在测站上测得后视、前视读数分别为a、b,则高差h=a-b。这里高差h是直接观测量a、b的函数。显然,当a、b存在误差时,h也受其影响而产生误差。这种关系称为误差传播,阐述这种函数关系的定律称为误差传播定律。误差传播定律随函数的不同而不同,下面按照从简到繁的函数形式来叙述。
5.3.1 倍乘函数
设有函数
![]()
式中,k为没有误差的常数;x为观测值。
当观测值x有误差Δx时,函数z的误差为Δz,即
![]()
式(5.10)减去式(5.9)得
![]()
对x进行n次观测,则有
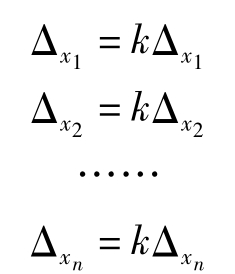
公式两边平方相加再除以n,则
![]()
当n→∞时,两边的极限值为
![]()
根据中误差定义可得

也就是说,观测值与一常数的乘积的中误差,等于观测值的中误差乘以该常数,亦即其中误差仍然保持倍乘关系。
【例5.2】在1∶500的地形图上测得两点之间的距离,图上的距离d=42.3mm,在地形图上量距中误差md=±0.2mm,求实地的距离D及中误差mD。
【解】

5.3.2 和或差函数
设有函数
![]()
当x与y分别含有真误差Δx与Δy时,则函数z也会产生真误差Δz,由式(5.12)可得
![]()
式(5.13)减去式(5.12)得
![]()
设x与y都观测了n次,则有

公式两边平方相加再除以n得
![]()
当n→∞时,两边的极限值为
![]()
由于这里x与y都是独立观测值,所以ΔxΔy也具有偶然误差的特性。根据偶然误差第四个特性,当n相当大时,[ΔxΔy]=0,故上式为
![]()
根据中误差定义可得
![]()
由式(5.14)推而广之,设函数z=x1+x2+…+xn,x1,x2,…,xn为独立观测值,它们的中误差为m1,m2,…,mn,则函数z的中误差mz为
![]()
由式(5.15)可知,和或差函数的中误差等于各个观测值中误差平方之和再开方。假设式(5.15)中
![]()
则
![]()
【例5.3】如图5.3所示的测站O,观测了α,β,γ三个角度,已知其中误差分别为12″,24″,24″,求角度δ的中误差
【解】
由图5.3可知
![]()
由误差传播率得
![]()
5.3.3 线性函数
设有独立观测值为L1,L2,…,Ln,常数k1,k2,…,kn,线性函数Z的关系为
![]()

图5.3
再设x1=k1L1,x2=k2L2,…,xn=knLn,则式(5.17)可变为
![]()
设Li观测值的中误差为mLi,则xi的中误差 =
=
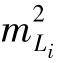 ,函数Z的中误差为
,函数Z的中误差为
![]()
式(5.18)的推导过程是先将线性函数简化为和或差的函数,再把每个变量化为倍数函数。由式(5.18)可知,线性函数中误差的平方等于各常数项平方与相应观测值中误差平方乘积之和。
【例5.4】如图5.4所示的三角形ABC中,以同精度观测三内角L1,L2,L3。其相应中误差为m,且观测值之间相互独立,试求:

图5.4
(1)三角形闭合差w的中误差mw;
(2)将闭合差平均分配后角A的中误差mA。
【解】
(1)三角形闭合差为
![]()
由和差函数误差传播律得
![]()
![]()
(2)平均分配闭合差后角A的表达式为

上式表明:闭合差分配后角A的中误差比闭合差分配前角A的中误差要小,精度提高了,说明了平差的意义。
5.3.4 一般函数
设有一般函数
![]()
式(5.19)中x1,x2,…,xn为未知量的直接观测值,它们的中误差为m1,m2,…,mn,f为关系式。则
![]()
式(5.20)中 ,
,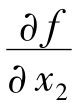 ,…,
,…, 为函数分别对x1,x2,…,xn求偏导数,且dz,dx1,dx2,…,dxn都可以用ΔZ,Δx1,Δx2…,Δxn这些微小的量来代替,同时令
为函数分别对x1,x2,…,xn求偏导数,且dz,dx1,dx2,…,dxn都可以用ΔZ,Δx1,Δx2…,Δxn这些微小的量来代替,同时令
![]()
则式(5.20)为
![]()
显然上式是一线性函数关系式。用式(5.18)可得
![]()
利用式(5.22)可以求得观测值任何函数的中误差。式(5.22)也称为误差传播定律的一般公式。
【例5.5】已知长方形的厂房,经过测量,其长x的观测值为90m,其宽y的观测值为50m,它们的中误差分别为2mm、3mm,求其面积及相应的中误差。
【解】
![]()

5.3.5 应用实例
1.水准测量的精度
1)每测站高差限差
每测站高差h=a-b,DS3型水准仪读数时估读毫米的误差范围为±3mm,即ma=mb =±3mm。由式(5.14)可得
![]()
即mh=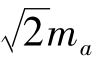 =±
=± ×3≈±4.2mm≈±5mm,故规定DS3型水准仪每测站两次高差之差范围为±5mm。
×3≈±4.2mm≈±5mm,故规定DS3型水准仪每测站两次高差之差范围为±5mm。
2)水准路线精度分析
设在A、B两点用水准仪测了n个测站,其中第i个测站测得的高差为hi,则A、B两点之间的高差h为
![]()
设各测站观测的高差是等精度的独立观测值,其中误差均为m站,即
![]()
由式(5.11)得
![]()
若水准路线是在地形平坦的地区进行的,前、后两立尺间的距离l大致相等。设A、B间距离为L,即两点测站数n=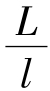 ,代入式(5.23)得
,代入式(5.23)得
![]()
若L=1km,l以km为单位,代入上式后,既得1km路线长的高差中误差m公里
![]()
当A、B的距离为Lkm时,A、B两点间的高差中误差mh为
![]()
若水准测量进行了往返观测,最后观测结果为往返测高差值取中数h-,则
![]()
设 m公里=
m公里= 公里,称为1km往返高差中数的中误差,则
公里,称为1km往返高差中数的中误差,则
![]()
由以上分析可看出,根据式(5.23),当各测站高差的观测精度相同时,水准测量高差中误差与测站数的平方根成正比。由(5.24)可知,当各测站距离大致相等时,水准测量高差中误差与距离的平方根成正比。
2.水平角测量的精度
1)DJ6型光学经纬仪测角中误差
DJ6型光学经纬仪一测回方向中误差为±6″,而一测回角值为两个方向值之差,故一测回角值的中误差为
![]()
2)测回之间较差
测回法测角时,各测回之间的较差的中误差应为其差值的中误差,即其差值中误差为
![]()
若以2倍中误差为限差,则有
![]()
故规定,DJ6型光学经纬仪用测回法测角时,各测回角值之差的范围不得超过±24″。
上一篇:怎样进行营运资金周转率分析
下一篇:呆账核销在会计上和税务上的差异性





.jpg)
.jpg)
