
实验十四 二阶动态电路的响应及其测试
一、实验目的
1.研究RLC串联电路的电路参数与其暂态过程的关系。
2.观察二阶电路在过阻尼、临界阻尼和欠阻尼三种情况下的响应波形,加深对二阶电路响应的认识和理解。
3.利用响应波形,计算二阶电路暂态过程的有关参数。
4.掌握观察动态电路状态轨迹的方法。
二、实验内容
1.RLC串联电路的研究
观察二阶电路的零输入响应和零状态响应由过阻尼到临界阻尼,最后到欠阻尼的变化过渡过程。改变电路参数时,记录ωd与δ的变化。
2.GCL并联电路的研究
观察二阶电路的零输入响应和零状态响应由过阻尼到临界阻尼,最后到欠阻尼的变化过渡过程。改变电路参数时,记录ωd与δ的变化。
三、实验设备与仪器
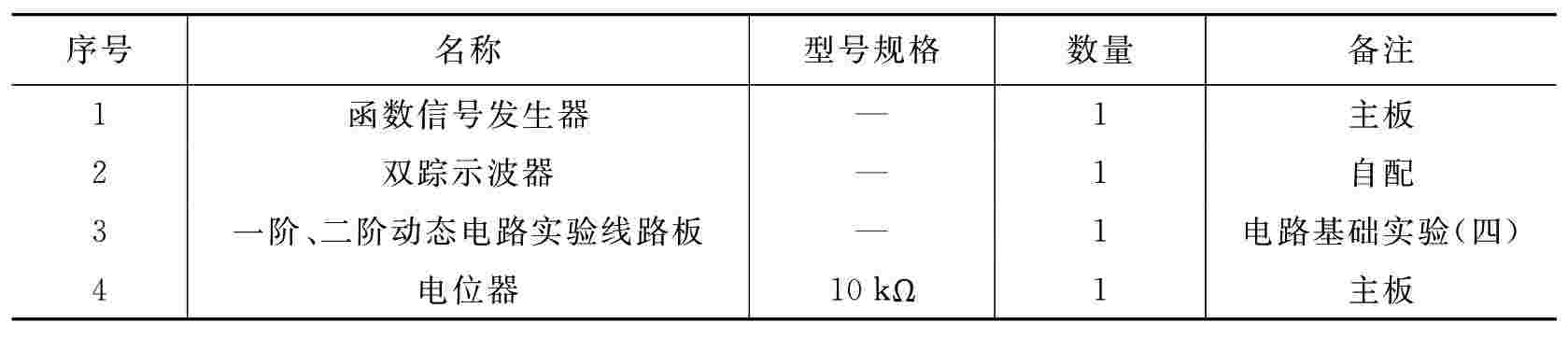
四、实验原理
用二阶微分方程描述的动态电路为二阶电路。一个二阶电路在方波正、负阶跃信号的激励下,可获得零状态与零输入响应,其响应的变化轨迹决定于电路的固有频率。
简单而典型的二阶电路是一个RLC串联电路和GCL并联电路,这二者之间存在着对偶关系。
1.RLC串联电路
(1)如图4-55所示的R、L、C串联电路是典型的二阶电路。电路的零输入响应只与电路的参数有关,对不同的电路参数,其响应有不同的特点:

图4-55 RLC串联电路
当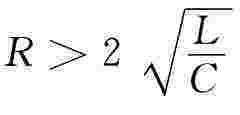 时,响应是非振荡性的,称为过阻尼情况,零输入响应为非振荡性的放电过程,零状态响应为非振荡性的充电过程。响应电压波形如图4-56所示。
时,响应是非振荡性的,称为过阻尼情况,零输入响应为非振荡性的放电过程,零状态响应为非振荡性的充电过程。响应电压波形如图4-56所示。
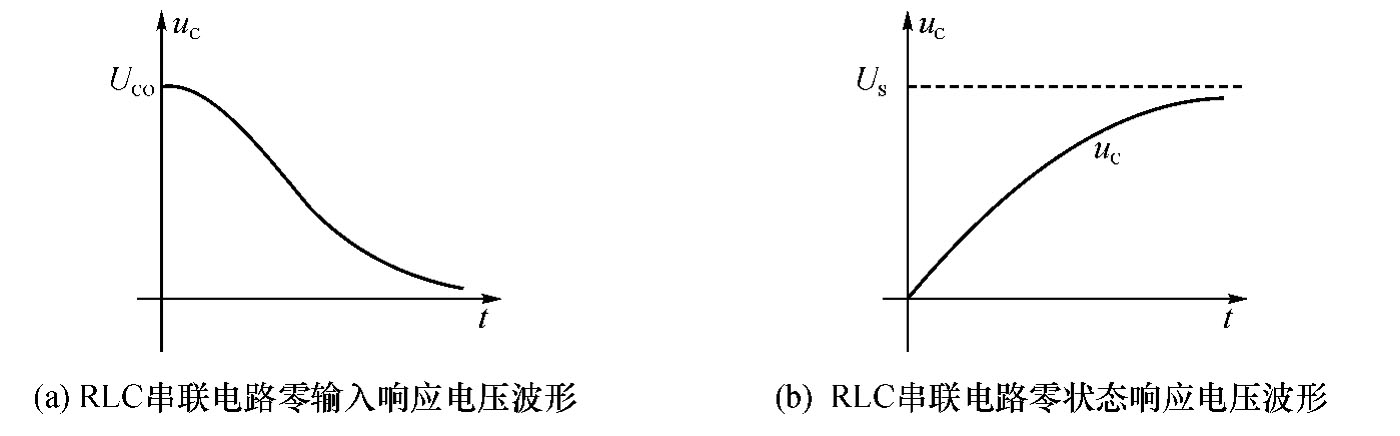
图4-56 过阻尼状态
当 时,零输入响应中的电压、电流具有衰减振荡的特点,称为欠阻尼状态,衰减系数
时,零输入响应中的电压、电流具有衰减振荡的特点,称为欠阻尼状态,衰减系数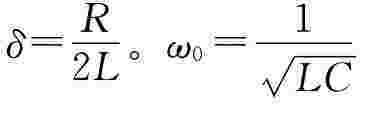 是在R=0情况下的振荡角频率,称为无阻尼振荡电路的固有角频率。在R≠0时,R、L、C串联电路的固有振荡角频率
是在R=0情况下的振荡角频率,称为无阻尼振荡电路的固有角频率。在R≠0时,R、L、C串联电路的固有振荡角频率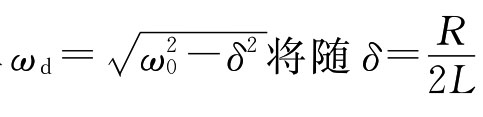 的增加而下降。零输入响应的过渡过程为振荡性的放电过程,零状态响应的过渡过程为振荡充电过程。其响应电压波形如图4-57所示。
的增加而下降。零输入响应的过渡过程为振荡性的放电过程,零状态响应的过渡过程为振荡充电过程。其响应电压波形如图4-57所示。
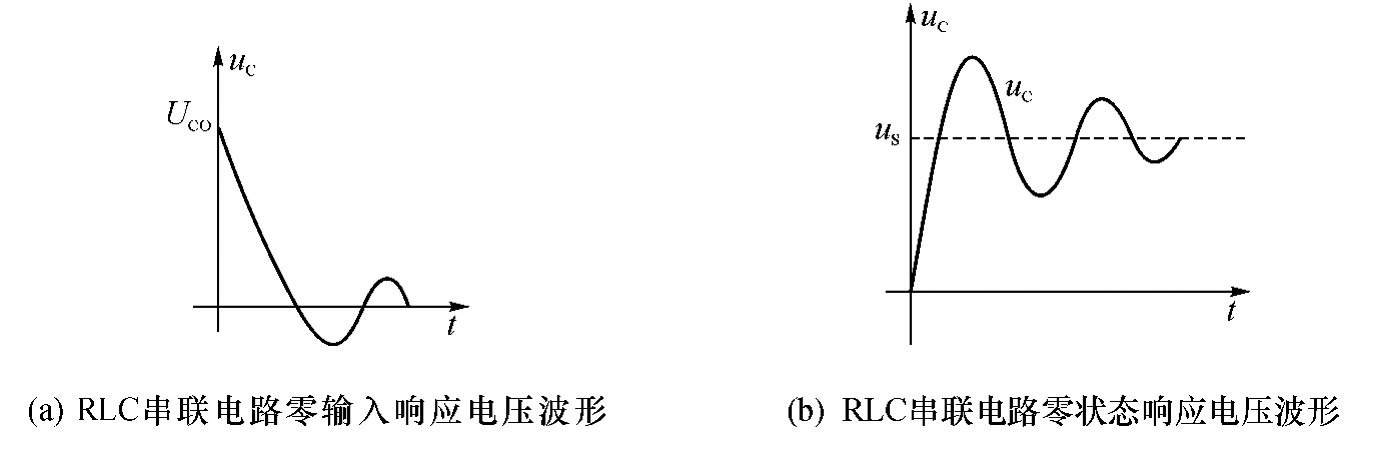
图4-57 欠阻尼状态
当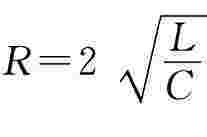 时,有
时,有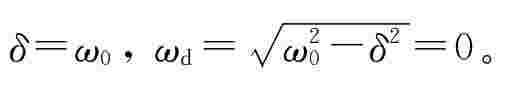 暂态过程介于非周期与振荡之间,响应临近振荡,称为临界状态,其本质属于非周期暂态过程。在临界情况下,放电过程是单调衰减过程,仍然属于非振荡。
暂态过程介于非周期与振荡之间,响应临近振荡,称为临界状态,其本质属于非周期暂态过程。在临界情况下,放电过程是单调衰减过程,仍然属于非振荡。
(2)欠阻尼状态下的衰减系数δ和振荡角频率ωd可以通过示波器观测电容、电压的波形求得。图4-58是RLC串联电路接至方波激励时,呈现衰减振荡暂态过程的波形。相邻两个最大值的间距为振荡周期Td,ωd=2π/Td,对于零输入响应,相邻两个最大值的比值为U1m/U2m=eδTd,所以衰减系数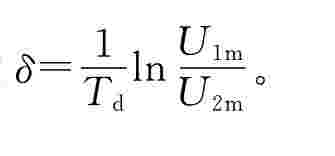
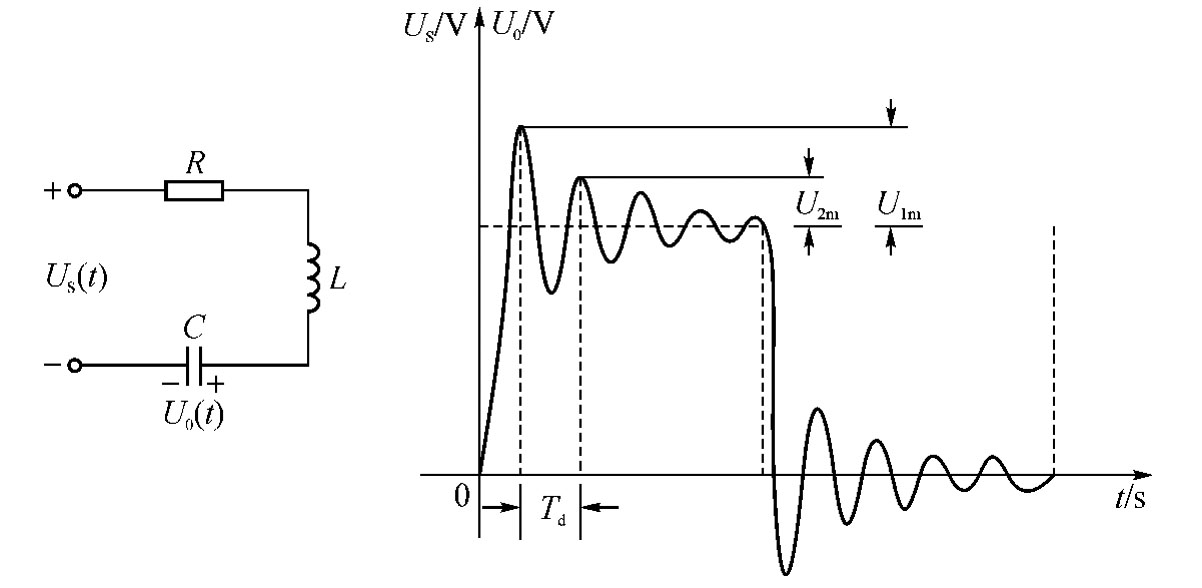
图4-58 RLC串联电路接至方波激励及衰减振荡的波形
除了在以上各图所示的u-t或i-t坐标系上研究动态电路的暂态过程以外,还可以在相平面作同样的研究工作。相平面也是直角坐标系,其横轴表示被研究的物理量x,纵轴表示被研究的物理量对时间的变化率dx/dt。由电路理论可知,对于RLC串联电路,可取电容电压uC、电感电流iL为两个状态变量。因为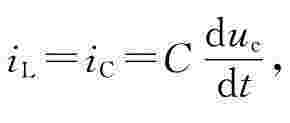 所以uC取为横坐标,iL取为纵坐标,构成研究该电路的状态平面。每一时刻的uC、iL,可用相平面上的某点表示,称为相迹点。uC、iL随时间变化的每一个状态可用相平面上的一系列相迹点表示。一系列相迹点相连得到的曲线,称为状态轨迹(或相轨迹)。用示波器显示动态电路状态轨迹的原理与显示李萨如图形完全一样,本实验中将RLC串联电路的uC、iL分别送入示波器的X轴输入和Y轴输入,便可得到状态轨迹。
所以uC取为横坐标,iL取为纵坐标,构成研究该电路的状态平面。每一时刻的uC、iL,可用相平面上的某点表示,称为相迹点。uC、iL随时间变化的每一个状态可用相平面上的一系列相迹点表示。一系列相迹点相连得到的曲线,称为状态轨迹(或相轨迹)。用示波器显示动态电路状态轨迹的原理与显示李萨如图形完全一样,本实验中将RLC串联电路的uC、iL分别送入示波器的X轴输入和Y轴输入,便可得到状态轨迹。
2.GCL并联电路
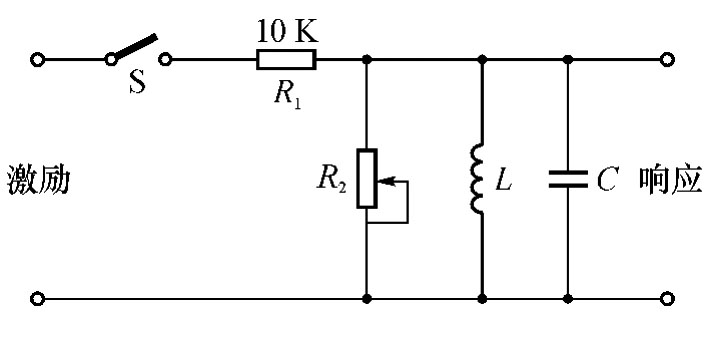
图4-59 GCL并联电路
如图4-59所示电路为GCL并联电路。电路的微分方程为: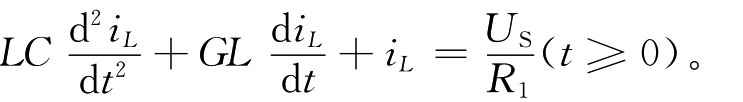
令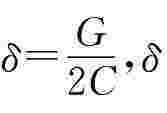 称为衰减系数
称为衰减系数 ω0称为固有频率;
ω0称为固有频率;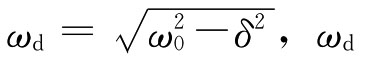 称为振荡角频率。
称为振荡角频率。
方程的解分三种情况:
δ>ω0,称为过阻尼状态,响应为非振荡性的衰减过程。
δ=ω0,称为临界阻尼状态,响应为临界过程。
δ<ω0,称为欠阻尼状态,响应为振荡性的衰减过程。
实验中,可通过调节电路的元件参数值,改变电路的固有频率ω0之值,从而获得单调地衰减和衰减振荡的响应,并可在示波器上观察到过阻尼、临界阻尼和欠阻尼这三种响应的波形,如图4-60和图4-61所示。
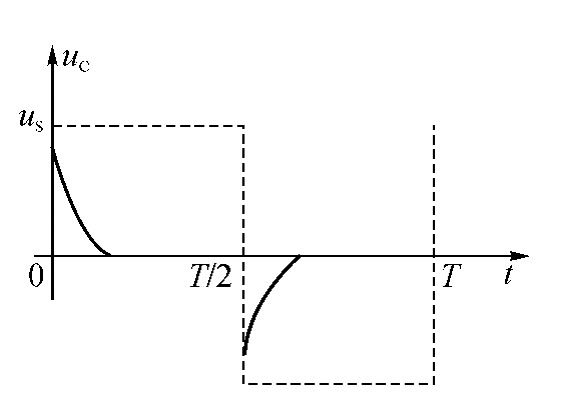
图4-60 GCL并联电路的过阻尼响应
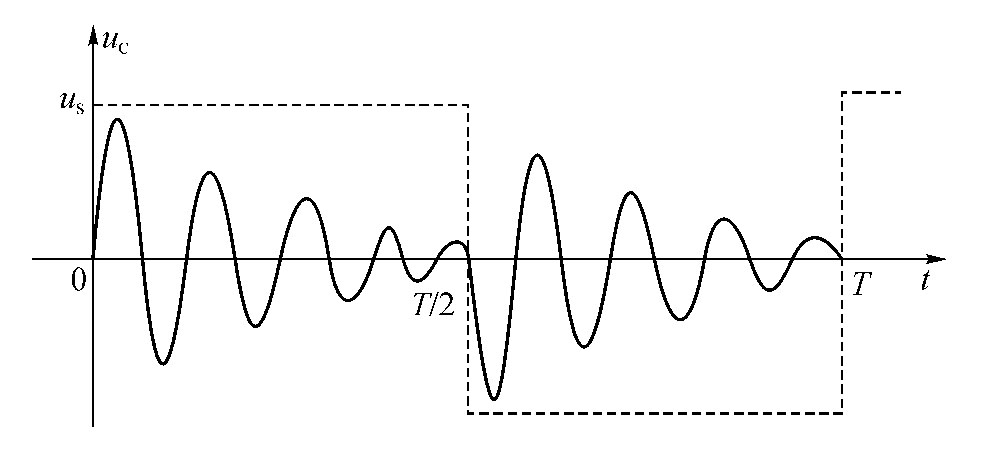
图4-61 GCL并联电路的欠阻尼响应
五、实验注意事项
1.调节R2时,要细心、缓慢,临界阻尼要找准。
2.实验前,请仔细阅读数字锁存示波器操作说明。
3.观察双踪时,显示要稳定;如不同步,可采用外同步法(看示波器说明)触发。
六、实验内容与步骤
1.RLC串联电路的研究
(1)动态电路板与实验十二相同,如图4-50所示。利用动态电路板中的元件与开关的配合作用,组成如图4-62所示的RLC串联电路。令取样电阻r=100Ω,L=10mH,C=1 000 pF,RL为10kΩ可调电阻器(元件箱)。令函数信号发生器的输出为Um=3V,f=1kHz的方波脉冲信号,通过同轴电缆线接至激励端;同时用同轴电缆线将激励端和响应输出端接至双踪示波器的YA和YB两个输入口。
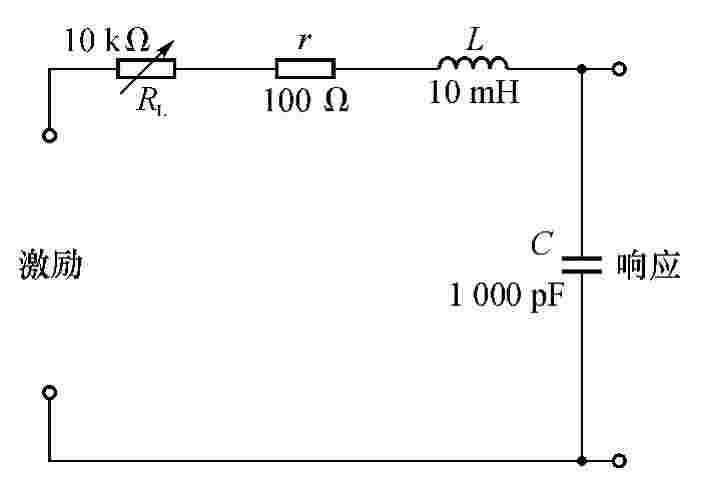
图4-62 RLC串联电路
(2)调节可变电阻器RL的值,观察二阶电路的零状态响应由过阻尼到临界阻尼,最后到欠阻尼的变化过渡过程,定性地描绘、记录响应的典型变化波形。
(3)调节RL使示波器荧光屏上呈现稳定的欠阻尼响应波形,用示波器光标测量按钮(cursor按钮)测出振荡周期Td,相邻两个最大值U1m、U2m,计算出此时电路的衰减常数δ和振荡角频率ωd(ωd=2π/Td,衰减系数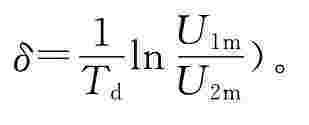
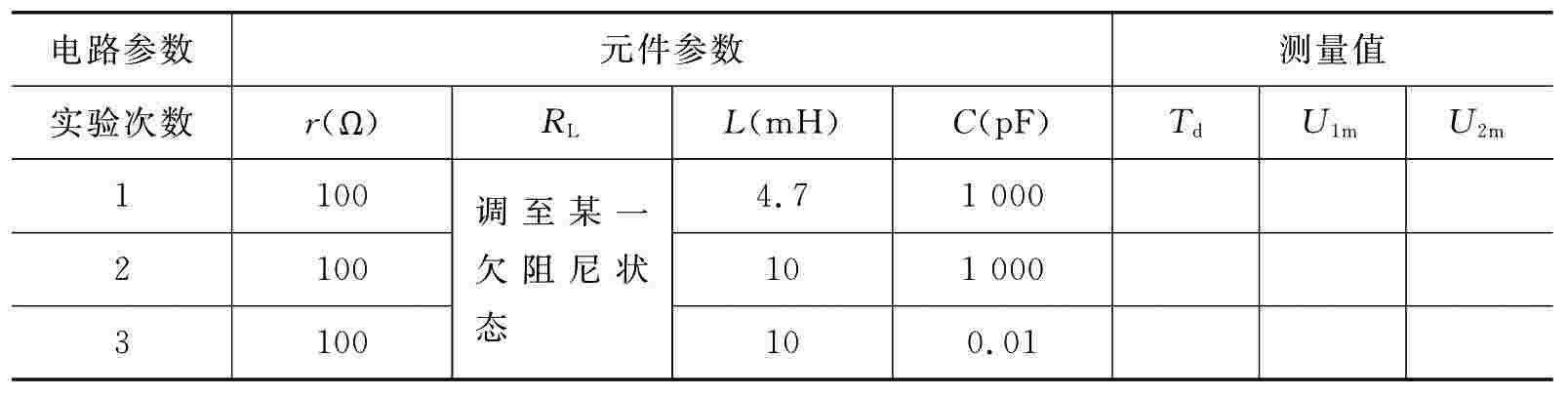
(4)改变一组电路常数,比如增减L或C的值,重复步骤2的测量并作记录。随后仔细观察改变电路参数时,ωd与δ的变化趋势并作记录。
表4-43 测量数据1
2.GCL并联电路的研究
(1)动态电路板与实验十二相同,如图4-50所示。利用动态电路板中的元件与开关的配合作用,组成如图4-63所示的GCL并联电路。令R1=10kΩ,L=10mH,C=1 000pF,R2为10kΩ电位器(可调电阻)。令函数信号发生器的输出为Umax=3V,f=1kHz的方波脉冲信号,通过同轴电缆线接至图的激励端;同时用同轴电缆线将激励端和响应输出端接至双踪示波器的YA和YB两个输入口。
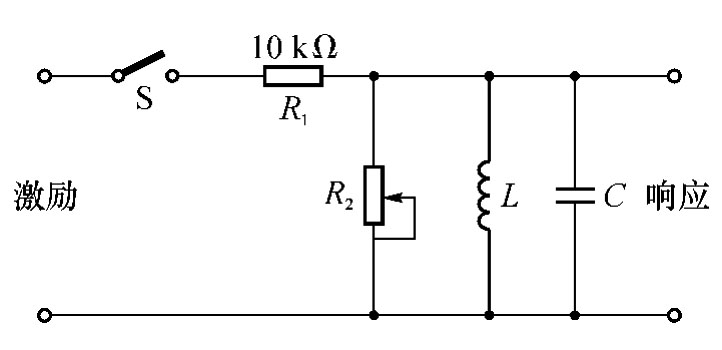
图4-63 GCL并联电路
(2)调节可变电阻器R2的值,观察二阶电路的零状态响应由过阻尼到临界阻尼,最后到欠阻尼的变化过渡过程,定性地描绘、记录响应的典型变化波形。
(3)调节R2使示波器荧光屏上呈现稳定的欠阻尼响应波形,用示波器光标测量按钮(cursor按钮)测出振荡周期Td,相邻两个最大值U1m、U2m,计算此时电路的衰减常数δ和振荡角频率ωd。
(4)改变一组电路常数,比如增减L或C之值,重复步骤2的测量并作记录。随后仔细观察改变电路参数时,ωd与δ的变化趋势并作记录。
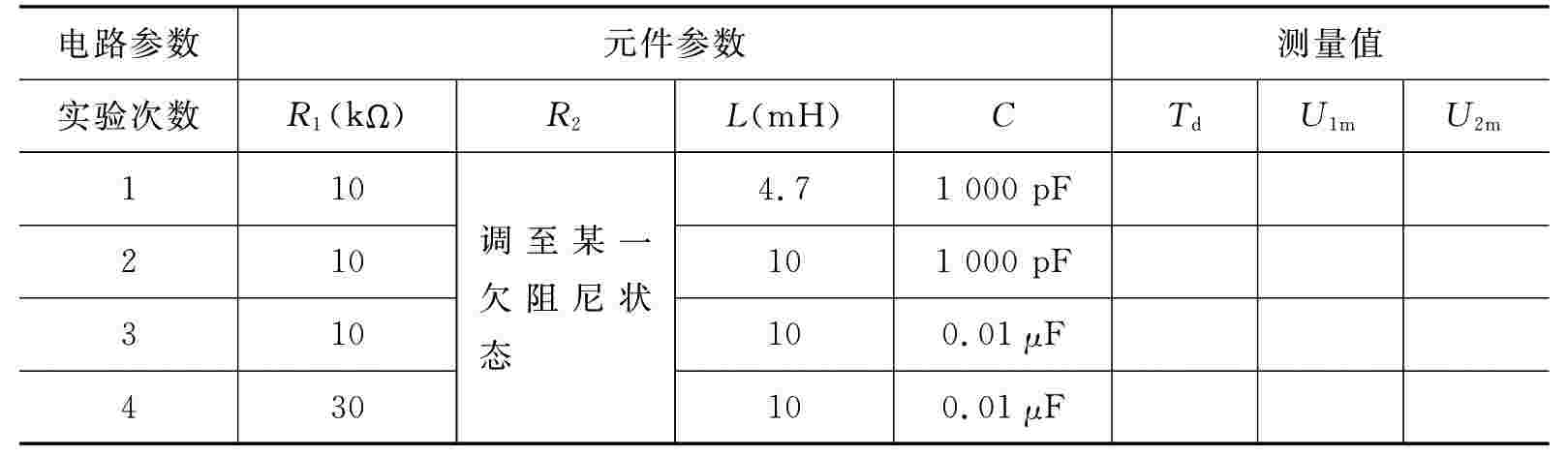
表4-44 测量数据2
七、实验报告要求
1.根据观测结果,在方格纸上描绘二阶电路过阻尼、临界阻尼和欠阻尼的响应波形。
2.测算欠阻尼振荡曲线上的衰减常数δ和振荡角频率ωd。
3.归纳总结电路元件参数的改变对响应变化趋势的影响。
八、实验思考题
1.根据二阶电路实验电路板元件的参数,计算处于临界阻尼状态的R2值。
2.在示波器荧光屏上,如何测得二阶电路零输入响应欠阻尼状态的衰减常数δ和振荡角频率ωd?
下一篇:公共管理学的理论基础





.jpg)
.jpg)
