灰色关联分析在事故成因分析中的应用

    7．3．3　灰色关联分析在事故成因分析中的应用

    灰色关联分析是一种多因素统计分析方法，它是以各因素的样本数据为依据用灰色关联度来描述因素间关系的强弱、大小和次序的。灰色关联分析对数据要求较低且计算量小，便于广泛应用，其核心是计算关联度。其计算步骤如下:

    1）确定分析序列

    在对所研究问题定性分析的基础上，确定一个因变量因素和多个自变量因素，设因变量数据构成参考序列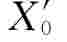，各自变量数据构成比较序列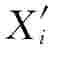（i＝1，2，…，n），n＋1个数据序列形成如下矩阵:

    

    其中，表示主元素，由于统计指标为事故的四项基本指标，故N＝4，即矩阵（7－13）的行代表事故指标，列代表主元素，矩阵本身表示一个主因素。

    2）事故指标的统计及指标的无量纲化

    对于每种事故形态，分别统计每个主因素确定的各主元素的事故数、死亡人数、受伤人数、直接经济损失四项指标，并按式（7－14）进行无量纲化计算。

    

    式中:x_ij——主元素i的第j个事故指标的无量纲化结果；

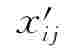    ——主元素i的第j个原始事故指标；

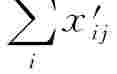    ——对应于该事故形态的原始事故指标j的总和。

    这样无量纲化后的指标是有意义的，反映的是事故指标j在该事故形态中总的比例，即可以看作对事故的影响程度。无量纲化后各因素序列形成如下矩阵:

    

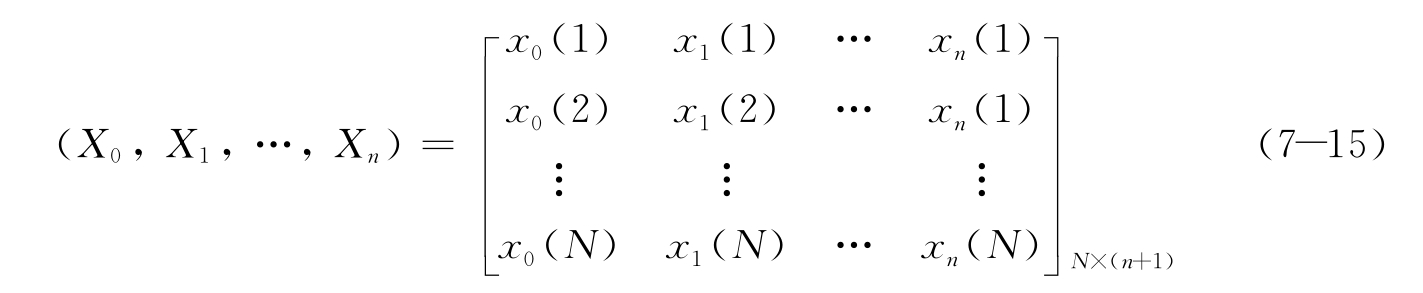
    3）确定参考序列

    对于每个主因素，可选最优样本数据作为参考序列，其关联度越大表示与事故越相关。其中第i个主元素为Xi＝（x_i（1），x_i（2），…，x_i（N））^T，i＝1，2，…，n，构造最优样本:

    

    其中

    

    4）求差序列、最大差和最小差

    计算（7－15）中第一列（参考序列）与其余各列（比较序列）对应值的绝对差值，形成如下绝对差值矩阵:

    

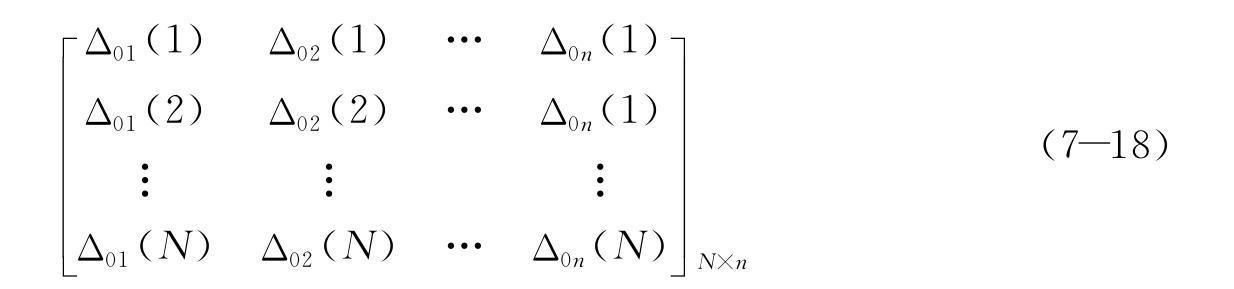
    其中

    

    绝对差值矩阵中最大数和最小数即为最大差和最小差:

    

    

    5）计算关联系数

    对绝对差值矩阵中数据作如下变换:

    

    得到关联系数矩阵:

    

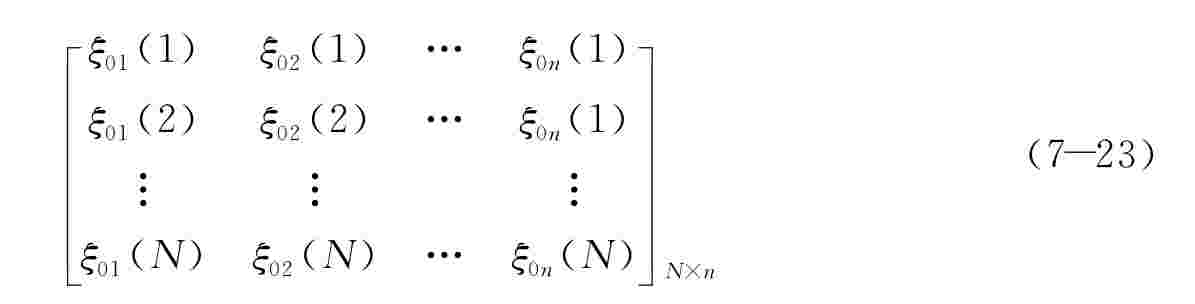
    式中分辨系数ρ在（0，1）取值，一般情况下依据（7－23）中的数据情况多在0．1至0．5取值，ρ越小越能提高关联系数间的差异，关系系数ξ⁰i（k）是不超过1的正数，Δ_0i（k）越小，ξ_0i（k）就越大，它反映第i个比较序列Xi与参考序列X⁰在第k期的关联程度。

    6）计算关联度

    比较序列X_i与参考序列X₀的关联程度是通过N个关联系数来反映的，一般关联度的计算采用求平均即可得到X_i与X₀的关联度:

    

    但对于本文而言，4项事故指标事故次数、死亡人数、受伤人数、直接经济损失，若采用取平均值的做法难以反映对事故频数和事故严重程度的影响，因而可以考虑采用加权平均来求关联度，各指标的权重采用德尔非法或层次分析法等确定，计算公式如式（7－25）:

    

    式中:w_k——指标k的权重。