力场和势函数

力场和势函数_分子医学导论

    一、力场和势函数

    对每一个模拟的蛋白质分子，都必须赋予一定的力场。根据量子力学的波恩奥本海默（Born－Oppenheimer）近似假设，即忽略电子运动，一个分子的能量可以近似看作构成分子的各个原子的空间坐标的函数，简单地讲就是分子的能量随分子构型的变化而变化，而描述这种分子能量和分子结构之间关系的就是分子力场函数（势函数）。分子力场函数来自实验结果的经验公式，对分子能量的模拟比较粗糙，但是相比于精确的量子力学从头计算方法，分子力场方法的计算量减少了数10倍，而且在适当的范围内，分子力场方法的计算精度与量子化学计算相差无几，根据小分子拟合的参数可推广到大分子体系，因此，对大分子复杂体系而言，分子力场方法是一套行之有效的方法。以分子力场为基础的分子力学计算方法、分子动力学等方法在分子模拟中有着广泛的应用。

    分子力场函数由以下几个部分构成。

    （1）键伸缩能（bond）构成分子的各个化学键在键轴方向上的伸缩运动所引起的能量变化（图18－3）。

    （2）键角弯曲能（bond angle）键角变化引起的分子能量变化（图18－4）。

    

    

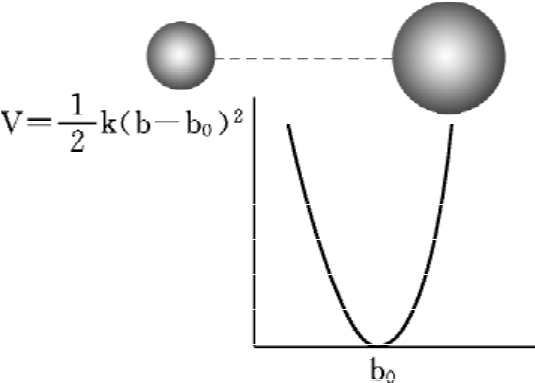
    图18－3　键伸缩能量

    

    

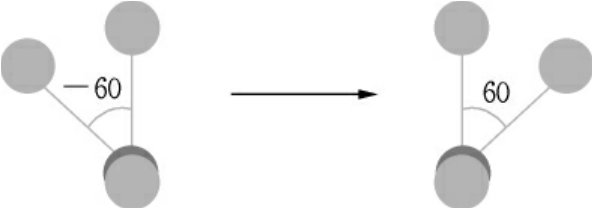
    图18－4　键角弯曲能量

    （3）二面角扭曲能（dihedral angel）单键旋转引起分子骨架扭曲所产生的能量变化（图18－5）。

    

    

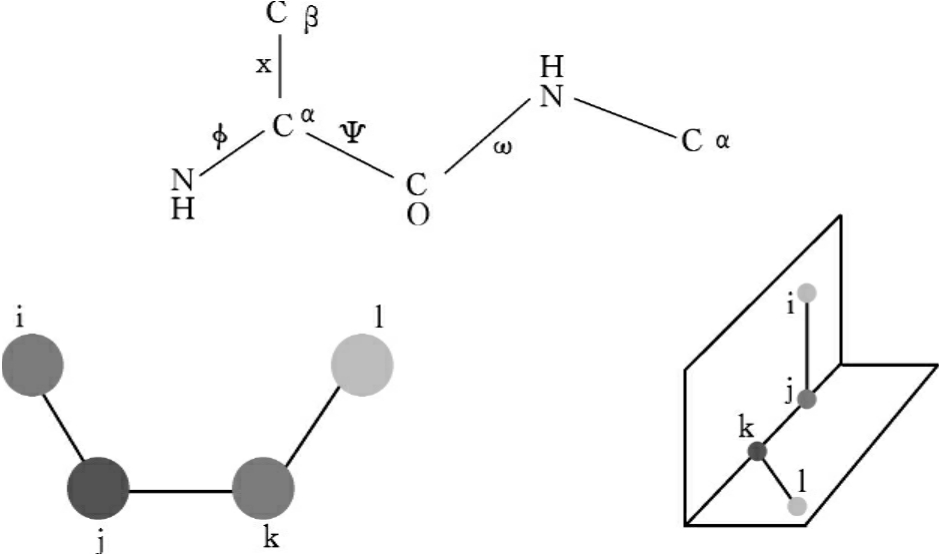
    图18－5　肽链主链中的二面角

    （4）非键相互作用（nonbonded interaction）包括范德华力（Van der Waals）、静电相互作用（Coulomb force）以及氢键等与能量有关的非键相互作用。

    一般常用Lennard－Jones12－6函数来描述范德华力：

    

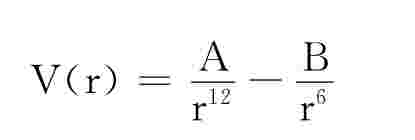
    Ａ＝４εσ¹²，Ｂ＝４ε⁶

    静电作用的常用表达函数为

    

    （5）交叉能量项上述作用之间耦合引起的能量变化。

    构成一套力场函数体系需要有一套联系分子能量和构型的函数，还需要给出各种不同原子在不同成键状况下的物理参数，比如正常的键长、键角、二面角等，这些力场参数多来自实验或者量子化学计算。

    以CVFF力场为例

    

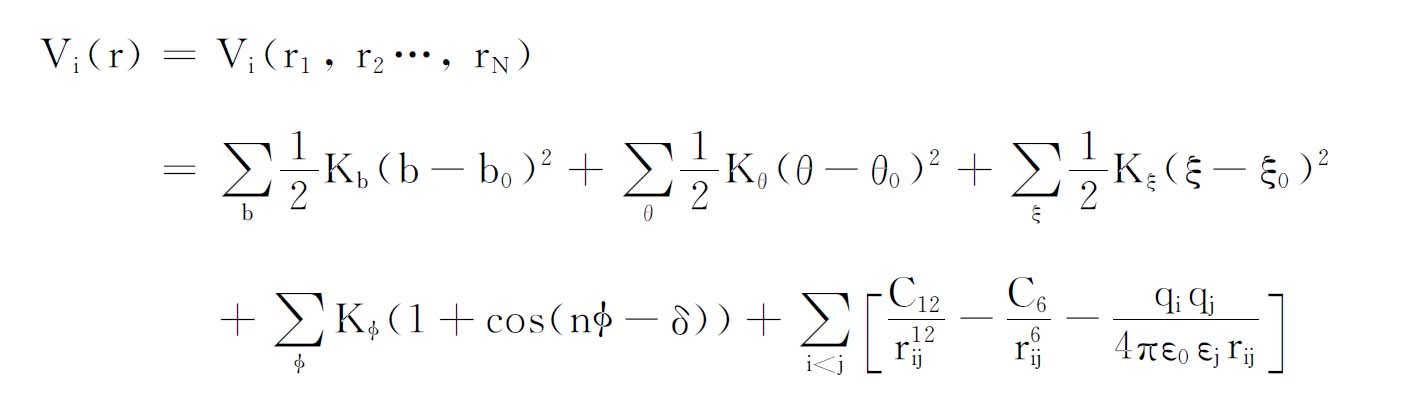
    其中，第一项

    

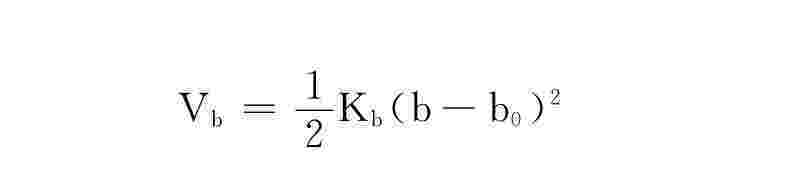
    为键伸缩能；第二项

    

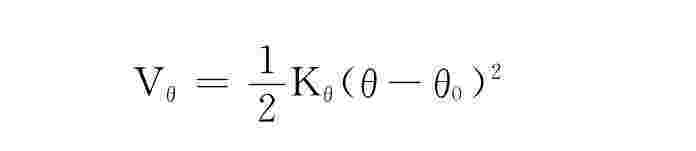
    为键角弯曲能；第三、四项

    

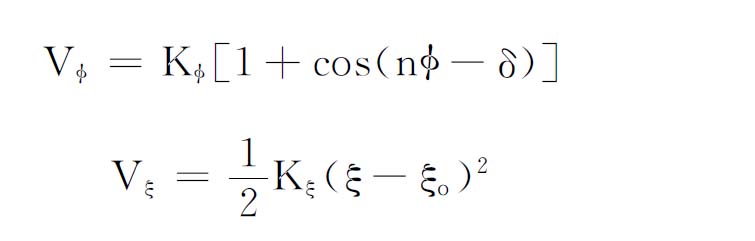
    分别为二面角扭曲能和非正常二面角扭曲能修正项；函数中最后一项为非键相互作用。